Una via efficace per cogliere la natura dei fenomeni ondulatori consiste nell’osservare sistemi nei quali si trasferisce energia senza trasporto netto di materia. Si consideri una boa vicina alla riva: al passaggio del treno d’onda essa sale e scende, ma non avanza verso la costa. A livello microscopico, le particelle d’acqua oscillano attorno a posizioni di equilibrio, rimanendo mediamente nello stesso intorno. Pertanto, ciò che si propaga non è il mezzo, bensì una perturbazione che si diffonde nel mezzo.

Quando la perturbazione si ripete con regolarità temporale, si parla di fenomeno periodico. In un solido elastico, ad esempio, un impulso meccanico applicato a un’estremità di una sbarra induce compressioni e dilatazioni che si propagano lungo l’asse del solido: dopo un intervallo finito, anche estremità lontane entrano in vibrazione, mentre la sezione iniziale torna in equilibrio (Figura 04.08-01). Se il materiale fosse rigidamente indeformabile, l’intero corpo si muoverebbe come un blocco; l’elasticità, invece, consente il propagarsi della perturbazione con particelle che oscillano intorno all’equilibrio senza migrare da una sezione all’altra.

Un comportamento analogo si osserva in una corda tesa eccitata trasversalmente all’estremità libera: il disturbo si sposta lungo la corda con una velocità definita, mentre i punti del mezzo oscillano perpendicolarmente alla direzione di propagazione (Figura 04.08-02). In un piano liquido, una goccia che cade genera circonferenze concentriche di perturbazione che si allargano dal punto di impatto.

Nei moti periodici le grandezze cinematiche, come spostamento, velocità e accelerazione di una particella, sono funzioni periodiche del tempo. Formalmente si scrive \( f(t) = f(t+T) \), dove \(T\) è il periodo di ripetizione:

\[f(t) = f(t + T),\]

Il periodo \(T\) è il tempo necessario a completare un ciclo (Figura 04.08-03). La frequenza è \( \nu = 1/T \) e misura il numero di cicli al secondo; l’unità del SI è l’hertz (Hz).

Un’onda monocromatica, o armonica, è descrivibile con una funzione sinusoidale che dipende sia dal tempo sia dalla posizione. Una rappresentazione tipica mette in evidenza l’andamento temporale in un punto fissato (Figura 04.08-03) e la dipendenza spaziale a tempo fissato (Figura 04.08-03). In tali condizioni valgono relazioni fondamentali tra grandezze ondulatorie, in particolare tra velocità di propagazione \(v\), lunghezza d’onda \(\lambda\) e frequenza \(\nu\):

\[v = \lambda \nu,\]

La lunghezza d’onda \(\lambda\) è la minima distanza tra due punti in fase, ad esempio due massimi consecutivi del segnale, ed equivale anche allo spazio percorso dall’onda nel tempo di un periodo \(T\) (Figura 04.08-03). È utile introdurre anche la pulsazione \( \omega = 2\pi \nu \) e il numero d’onda \( k = 2\pi/\lambda \): per un’onda armonica una forma esplicita è \( \psi(x,t) = A \cos(kx - \omega t + \phi_{0}) \), dalla quale segue la velocità di fase \( v = \omega/k \), coerente con la (\[v = \lambda \nu,\]).

I fenomeni ondulatori possono coinvolgere non solo spostamenti meccanici, ma anche campi fisici che oscillano nel tempo. Un caso rilevante è quello delle onde elettromagnetiche, nelle quali i vettori campo elettrico e magnetico variano periodicamente e si autosostengono nella propagazione (Figura 04.08-07). La luce è un esempio di radiazione elettromagnetica e manifesta caratteristiche ondulatorie analoghe, come interferenza e diffrazione.

La classificazione principale distingue secondo l’orientamento della vibrazione rispetto alla direzione di propagazione:

• onde trasversali, in cui le oscillazioni sono perpendicolari alla direzione di avanzamento (Figura 04.08-04); esempi: la corda tesa (Figura 04.08-07) e (Figura 04.08-02), le increspature superficiali nei liquidi, le onde elettromagnetiche (Figura 04.08-07);
• onde longitudinali, con vibrazione parallela alla direzione di propagazione (Figura 04.08-04); esempi: compressioni e rarefazioni in una sbarra elastica (Figura 04.08-01), le perturbazioni di pressione e densità che viaggiano nei gas (Figura 04.08-07), ossia le onde sonore.

La propagazione trasferisce l’oscillazione a regioni contigue del mezzo. I punti che condividono lo stesso stato di vibrazione (uguale fase) individuano superfici d’onda. Se la sorgente è puntiforme e il fenomeno si svolge in un piano, tali superfici sono circonferenze concentriche; nello spazio tridimensionale diventano sfere concentriche. Le direzioni ortogonali alle superfici d’onda vengono talvolta descritte come raggi.

Tutte le particelle di un mezzo investito da un’onda elastica armonica riproducono la legge di oscillazione imposta dalla sorgente, con la medesima frequenza e con eventuali differenze di fase legate alla distanza. In (Figura 04.08-03) è illustrata la legge di propagazione di un’onda monocromatica in funzione del tempo e della distanza dalla sorgente.

Per il principio di conservazione dell’energia, la propagazione ondulatoria trasporta energia dal generatore verso il mezzo circostante. L’energia associata al moto ondulatorio, indicata nelle (\Delta \nu = \nu - \nu_{s} = \nu_{s} \left( -\frac{u_{s}}{v + u_{s}} \right)) oppure (E = E_{k} + U = 0 + \frac{1}{2} \omega^{2} m A^{2} = \frac{1}{2} \omega^{2} m A^{2}), si trasferisce lungo la direzione di avanzamento. Si definisce intensità l’energia trasportata nell’unità di tempo attraverso l’unità di superficie posta perpendicolarmente alla direzione di propagazione; nel SI essa si misura in W/m². In molte onde armoniche, in assenza di dissipazione, l’intensità è proporzionale al quadrato dell’ampiezza dell’oscillazione.

Le onde si propagano in tre dimensioni. In un mezzo isotropo e per una sorgente puntiforme, i fronti d’onda sono sferici (Figura 04.08-05). La potenza totale irradiata si distribuisce su superfici la cui area cresce con la distanza; di conseguenza, l’intensità decresce come l’inverso dell’area del fronte:

• per fronti sferici di raggio \(r\), \( A(r) = 4\pi r^{2} \) e dunque \( I(r) \propto r^{-2} \) (legge dell’inverso del quadrato);
• per fronti approssimativamente piani, l’area efficace non varia con \(r\) e l’intensità rimane pressoché costante lungo la direzione di propagazione (Figura 04.08-06).

Un’ultima proprietà cruciale concerne la direzionalità. Quanto più piccola è la lunghezza d’onda rispetto alle dimensioni dell’apertura o della sorgente, tanto più marcato è il collimamento del fascio per effetto della ridotta diffrazione: a frequenze elevate (per esempio nel dominio dei MHz per gli ultrasuoni o per onde elettromagnetiche a microonde e oltre) si ottengono fasci stretti assimilabili a “raggi”. In termini qualitativi, a parità di geometria della sorgente, la riduzione di \(\lambda\) aumenta la direzionalità del campo irradiato.

In sintesi, i fenomeni ondulatori descrivono la propagazione nel tempo e nello spazio di una perturbazione periodica, con trasporto di energia e, tipicamente, senza trasporto netto di materia. La relazione \( v=\lambda\nu \), le grandezze di fase, frequenza e lunghezza d’onda, e le proprietà geometriche dei fronti d’onda costituiscono gli elementi essenziali per interpretarne la dinamica.

Image Gallery

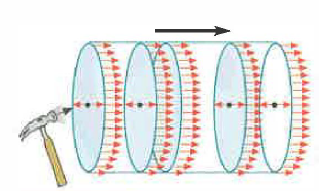
Vibrazione elastica in una sbarra

Vibrazione elastica che si propagain una sbarra metallica. Tutte le sezioni della sbarra sono sollecitatea vibrare in tempi successivi.La perturbazione è di tipo longitudinale.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

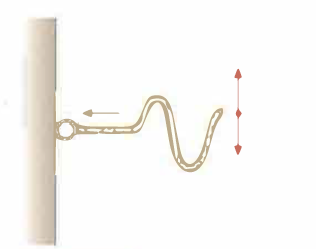
Vibrazione elastica in una corda

Vibrazione elastica che si propaga lungo una corda. La perturbazione è di tipo trasversale.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

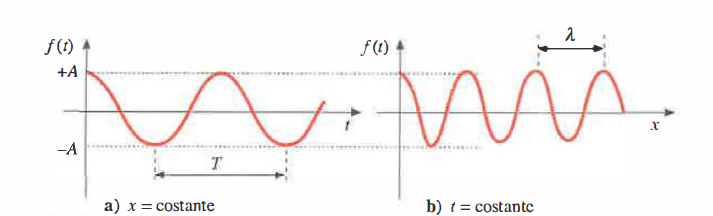
Legge di propagazione di un’onda

Rappresentazione grafica della legge di propagazione di un’onda monocromatica. In (a) è mostrata l’oscillazione nel tempo della generica grandezza f(t) in un punto determinato dello spazio. Il tempo tra due massimi (o minimi) successivi definisce il periodo T della vibrazione. In (b) è mostrata un’istantanea dello stato di vibrazione della grandezza f(t) in funzione della distanza dall’origine. La distanza tra due massimi (o minimi) successivi definisce la lunghezza d’onda λ della vibrazione.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Legge di propagazione di un’onda

Rappresentazione grafica della legge di propagazione di un’onda monocromatica. In (a) è mostrata l’oscillazione nel tempo della generica grandezza f(t) in un punto determinato dello spazio. Il tempo tra due massimi (o minimi) successivi definisce il periodo T della vibrazione. In (b) è mostrata un’istantanea dello stato di vibrazione della grandezza f(t) in funzione della distanza dall’origine. La distanza tra due massimi (o minimi) successivi definisce la lunghezza d’onda λ della vibrazione.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Legge di propagazione di un’onda

Rappresentazione grafica della legge di propagazione di un’onda monocromatica. In (a) è mostrata l’oscillazione nel tempo della generica grandezza f(t) in un punto determinato dello spazio. Il tempo tra due massimi (o minimi) successivi definisce il periodo T della vibrazione. In (b) è mostrata un’istantanea dello stato di vibrazione della grandezza f(t) in funzione della distanza dall’origine. La distanza tra due massimi (o minimi) successivi definisce la lunghezza d’onda λ della vibrazione.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Legge di propagazione di un’onda

Rappresentazione grafica della legge di propagazione di un’onda monocromatica. In (a) è mostrata l’oscillazione nel tempo della generica grandezza f(t) in un punto determinato dello spazio. Il tempo tra due massimi (o minimi) successivi definisce il periodo T della vibrazione. In (b) è mostrata un’istantanea dello stato di vibrazione della grandezza f(t) in funzione della distanza dall’origine. La distanza tra due massimi (o minimi) successivi definisce la lunghezza d’onda λ della vibrazione.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

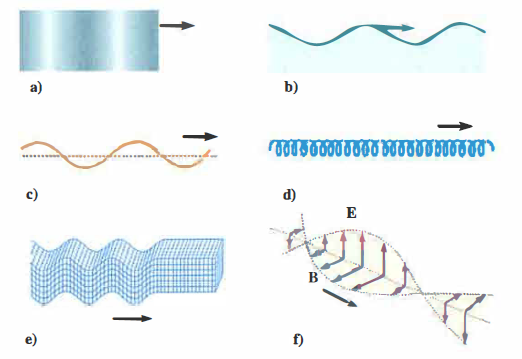
Fenomeni ondulatori

Alcuni tra i principali fenomeni ondulatori. (a) Un’onda sonora: ad esempio la vibrazione di un diapason mette in moto le molecole di un gas, le quali oscillano di moto armonico intorno alla posizione di equilibrio creando rarefazioni e addensamenti delle molecole. (b) L’onda superficiale che si propaga all’interfaccia liquido-aria. (c) Un’onda lungo una corda fatta oscillare. (d) Un’onda attraverso una molla. (e) Un tipo di onda sismica (onda S). (f) Un’onda elettromagnetica.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

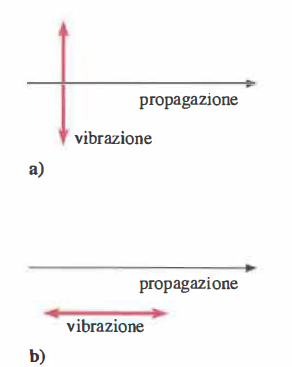
Vibrazioni trasversali e longitudinali

Rappresentazione schematica di: (a) una vibrazione trasversale e (b) una vibrazione longitudinale.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Fenomeni ondulatori

Alcuni tra i principali fenomeni ondulatori. (a) Un’onda sonora: ad esempio la vibrazione di un diapason mette in moto le molecole di un gas, le quali oscillano di moto armonico intorno alla posizione di equilibrio creando rarefazioni e addensamenti delle molecole. (b) L’onda superficiale che si propaga all’interfaccia liquido-aria. (c) Un’onda lungo una corda fatta oscillare. (d) Un’onda attraverso una molla. (e) Un tipo di onda sismica (onda S). (f) Un’onda elettromagnetica.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Vibrazione elastica in una corda

Vibrazione elastica che si propaga lungo una corda. La perturbazione è di tipo trasversale.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Fenomeni ondulatori

Alcuni tra i principali fenomeni ondulatori. (a) Un’onda sonora: ad esempio la vibrazione di un diapason mette in moto le molecole di un gas, le quali oscillano di moto armonico intorno alla posizione di equilibrio creando rarefazioni e addensamenti delle molecole. (b) L’onda superficiale che si propaga all’interfaccia liquido-aria. (c) Un’onda lungo una corda fatta oscillare. (d) Un’onda attraverso una molla. (e) Un tipo di onda sismica (onda S). (f) Un’onda elettromagnetica.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Vibrazioni trasversali e longitudinali

Rappresentazione schematica di: (a) una vibrazione trasversale e (b) una vibrazione longitudinale.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Vibrazione elastica in una sbarra

Vibrazione elastica che si propagain una sbarra metallica. Tutte le sezioni della sbarra sono sollecitatea vibrare in tempi successivi.La perturbazione è di tipo longitudinale.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Fenomeni ondulatori

Alcuni tra i principali fenomeni ondulatori. (a) Un’onda sonora: ad esempio la vibrazione di un diapason mette in moto le molecole di un gas, le quali oscillano di moto armonico intorno alla posizione di equilibrio creando rarefazioni e addensamenti delle molecole. (b) L’onda superficiale che si propaga all’interfaccia liquido-aria. (c) Un’onda lungo una corda fatta oscillare. (d) Un’onda attraverso una molla. (e) Un tipo di onda sismica (onda S). (f) Un’onda elettromagnetica.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Legge di propagazione di un’onda

Rappresentazione grafica della legge di propagazione di un’onda monocromatica. In (a) è mostrata l’oscillazione nel tempo della generica grandezza f(t) in un punto determinato dello spazio. Il tempo tra due massimi (o minimi) successivi definisce il periodo T della vibrazione. In (b) è mostrata un’istantanea dello stato di vibrazione della grandezza f(t) in funzione della distanza dall’origine. La distanza tra due massimi (o minimi) successivi definisce la lunghezza d’onda λ della vibrazione.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

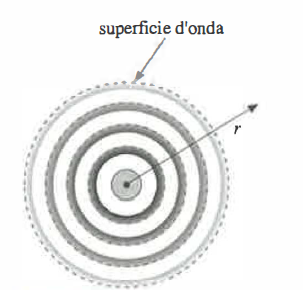
Superficie d’onda circolare o sferica

Rappresentazione schematica di una superficie d’onda circolare (o sferica). Tutti i punti della superficie d’onda vibrano in concordanza di fase. Le ampiezze decrescenti, in corrispondenza delle successive superfici d’onda, sono evidenziate da variazioni di densità di grigio. Viene indicata la distanza r dalla sorgente.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

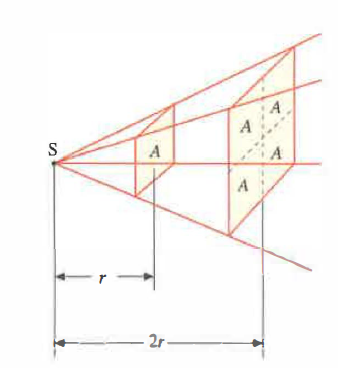
Distribuzione spaziale dell’intensità sonora

Distribuzione spaziale dell’intensità sonora. Se la distanza raddoppia, l’area A attraversata dall’energia dell’onda sonora diventa 4 volte maggiore e quindi l’intensità dell’onda diminuisce di 4 volte.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.