Moto dei fluidi: portata ed equazione di continuità
Definizione
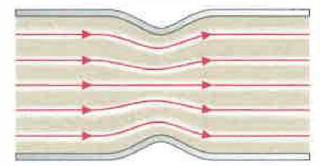
Descrivere il moto di un fluido richiede un’impostazione campistica: a ogni punto dello spazio e a ogni istante si associano grandezze come densità, pressione e velocità. I campi scalari di densità e pressione rappresentano, rispettivamente, la distribuzione della massa e delle forze interne, mentre lo stato di moto è descritto da un campo vettoriale di velocità. Nella (Figura 03.03-01) è illustrato un esempio: le linee tracciate, tangenti in ogni punto al vettore velocità locale, sono le linee di corrente (o linee di flusso). In regime stazionario tali linee coincidono con le traiettorie delle particelle, poiché la velocità dipende dalla posizione ma non esplicitamente dal tempo.
Il quadro si semplifica in condizioni stazionarie: per un dato punto del dominio, tutte le particelle che lo attraversano hanno identica velocità in modulo e direzione. In questa impostazione, salvo un breve richiamo finale a casi più generali, ci limiteremo a moti stazionari. Poiché misurare direttamente la velocità locale di ciascuna particella non è pratico, è utile introdurre una grandezza integrale di semplice determinazione sperimentale: la portata, spesso indicata anche come flusso volumetrico e denotata con Q. Per un condotto e una sua sezione trasversale S, si definisce portata il volume V di fluido che attraversa S nell’unità di tempo.
Le unità di misura più impiegate sono:
- SI: m³/s;
- CGS: cm³/s;
- unità pratiche: L/s = 1 000 cm³/s, L/min.
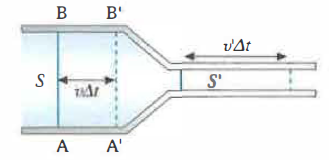
Consideriamo un tratto di condotto di sezione S nel quale la velocità ha modulo uniforme v e direzione perpendicolare alla sezione. Le particelle che si trovano inizialmente sul piano AB (Figura 03.03-02) si spostano, in un intervallo di tempo Δt, di una distanza vΔt; il prisma fluido compreso tra i piani AB e A′B′ possiede volume V = S v Δt. Per definizione, la portata risulta quindi:
\[ Q = \frac{V}{\Delta t} = \frac{S v \Delta t}{\Delta t} = S v \]
La definizione è generale e non vincolata alla natura del fluido né alla geometria del condotto. Quando la velocità non è perfettamente uniforme sulla sezione, è conveniente utilizzare la forma integrale: \[ Q = \iint_S \mathbf{v}\cdot \mathbf{\hat{n}}\, \mathrm{d}S, \] dove \(\mathbf{\hat{n}}\) è il versore normale alla sezione orientato secondo il verso di attraversamento. Si introduce così la velocità media sulla sezione, \[ \bar{v} = \frac{1}{S}\iint_S \mathbf{v}\cdot \mathbf{\hat{n}}\, \mathrm{d}S, \] per la quale, per definizione, vale ancora \(Q = S\,\bar{v}\). Questa relazione consente di collegare misure globali (Q) a grandezze locali (profili di velocità).
Dal principio di conservazione della massa discende l’equazione di continuità. Nel caso di moto stazionario di un fluido incomprimibile all’interno di un condotto rigido e senza perdite, la portata è identica in ogni sezione. Se il condotto presenta variazioni di area – come schematizzato in (Figura 03.03-02) –, uguagliando le portate nelle due sezioni si ottiene:
\[ S v = S' v' \quad \text{ossia} \quad \frac{v}{v'} = \frac{S'}{S}, \quad \text{in generale} \quad S v = \text{costante} \]
Ne segue che, a parità di portata, la velocità cresce nelle strozzature e diminuisce nelle dilatazioni: le velocità in sezioni differenti risultano inversamente proporzionali alle aree corrispondenti. Un’interpretazione equivalente si ottiene introducendo il concetto di tubo di corrente, costituito dall’inviluppo di linee di corrente: per un fluido incomprimibile in regime stazionario, la portata che attraversa ogni sezione del tubo di corrente rimane costante.
Estensioni utili: per flussi comprimibili ma stazionari in un condotto con moto prevalentemente unidimensionale, la continuità si scrive \(\rho S v = \text{costante}\), con \(\rho\) densità locale. In forma differenziale, la conservazione della massa è espressa da \[ \frac{\partial \rho}{\partial t} + \nabla\cdot(\rho \mathbf{v}) = 0, \] che, nel caso incomprimibile (\(\rho=\) costante), si riduce a \(\nabla\cdot \mathbf{v} = 0\). Queste formulazioni permettono di trattare sia regimi stazionari sia situazioni non stazionarie.
Esempio numerico. Un fluido incomprimibile scorre in un condotto che passa da S = 2,0 cm² a S′ = 0,80 cm². La portata è Q = 120 cm³/min. La velocità media nella prima sezione è \(\bar{v} = Q/S = 60\,\text{cm/min} \, / \, 2,0\,\text{cm}^2 = 30\,\text{cm/min}\). Dalla formual (\[S v = S' v' \quad \text{ossia} \quad \frac{v}{v'} = \frac{S'}{S}, \quad \text{in generale} \quad S v = \text{costante} \]) segue \(\bar{v}' = Q/S' = 120\,\text{cm}^3/\text{min} \, / \, 0,80\,\text{cm}^2 = 150\,\text{cm/min}\). Come previsto, la velocità cresce nella sezione più piccola mantenendo invariata la portata.