Gas perfetti
Definizione
Un gas in condizioni ordinarie può essere descritto, con buona approssimazione, come un insieme di atomi o molecole che occupano un volume trascurabile e interagiscono tra loro solo mediante urti elastici. Questo modello, che trascura le forze intermolecolari a distanza e l’estensione finita delle particelle, definisce il cosiddetto gas perfetto (o ideale). In tale quadro, lo stato termodinamico è specificato da quattro grandezze macroscopiche: pressione p, volume V, temperatura T e densità ρ. Le relazioni sperimentali tra queste variabili, verificate in condizioni di equilibrio e in trasformazioni controllate, sono particolarmente semplici per gas rarefatti e a temperature elevate, cioè lontane dalla liquefazione: in questo limite valgono le leggi dei gas perfetti.
In prima approssimazione, le deviazioni dal comportamento ideale sono misurate dal fattore di comprimibilità \(Z = \frac{pV}{nRT}\), che per un gas perfetto è pari a 1; per gas reali Z si discosta dall’unità in prossimità dell’area di condensazione o ad alte pressioni. Quando l’ipotesi di non interazione e di volume molecolare trascurabile è adeguata, le leggi seguenti si applicano con elevata accuratezza.
Leggi sperimentali fondamentali
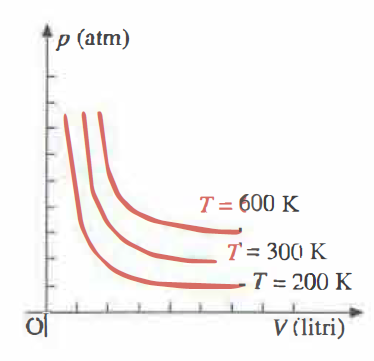
Legge di Boyle (trasformazione isoterma per una data massa di gas):
\[ p V = \text{costante.} \]
Prima legge di Gay-Lussac (riscaldamento a pressione costante): il volume a t °C è legato al volume a 0 °C da
\[ V_t = V_0 (1 + \alpha t) \]
Seconda legge di Gay-Lussac (riscaldamento a volume costante): la pressione a t °C è legata alla pressione a 0 °C da
\[ p_t = p_0 (1 + \beta t) \]
Dalle due leggi di Gay-Lussac si deduce che i coefficienti di dilatazione sono uguali, \(\alpha = \beta\), e, per gas ideali, indipendenti dalla specie chimica. L’estrapolazione lineare porta a un valore comune:
\[ \alpha = \frac{1}{273^\circ \mathrm{C}} \]
Il valore moderno, coerente con la definizione della scala Kelvin, è più precisamente \(1/273{,}15 \,^\circ\mathrm{C}^{-1}\); la linearità è un’ottima approssimazione nel regime di gas perfetto.
Unificazione delle leggi e trasformazioni elementari
Le tre leggi precedenti si combinano in un’unica relazione tra lo stato iniziale \((p_0, V_0, 0\,^\circ\mathrm{C})\) e lo stato finale \((p, V, t\,^\circ\mathrm{C})\), passando attraverso trasformazioni elementari:
\[ \begin{array}{lcccc} \text{condizioni iniziali (I)} & p_0 & V_0 & 0^\circ \mathrm{C} \\ \text{dopo un'isoterma (II)} & p' & V & 0^\circ \mathrm{C} \\ \text{dopo un'isocora (III)} & p & V & t^\circ \mathrm{C} \\ \text{condizioni finali} & p & V & t^\circ \mathrm{C} \end{array} \]
Dalla (I) alla (II) vale Boyle: \(p_0V_0 = p'V\). Dalla (II) alla (III), a volume costante, si applica la seconda legge di Gay-Lussac:
\[ p = p' (1 + \alpha t) \]
Eliminando \(p'\) si ottiene l’equazione di stato per una data massa di gas:
\[ p V = p_0 V_0 (1 + \alpha t) \]
Scala termometrica assoluta ed equazione dei gas perfetti
Introducendo la temperatura assoluta \(T\) tramite la relazione approssimata \(T = 273^\circ + t\) (in forma moderna: \(T[\mathrm{K}] = t[^\circ\mathrm{C}] + 273{,}15\)), l’equazione precedente si riscrive come:
\[ p V = \frac{p_0 V_0}{273^\circ} T = n R T \]
dove \(n\) è la quantità di sostanza (in moli) e \(R\) è la costante universale dei gas, uguale per tutti i gas ideali. La legge di Avogadro afferma che volumi uguali di gas diversi, alla stessa temperatura e pressione, contengono lo stesso numero di molecole. Una grammomolecola (oggi semplicemente “mole”) contiene \(N_A = 6{,}022 \times 10^{23}\) particelle. Conseguentemente, a 0 °C e 1 atmosfera, una mole di gas perfetto occupa un volume molare \(V_0 = 22{,}41\) L (Figura 05.09-01). Si noti che con lo standard IUPAC a 1 bar il volume molare è \(22{,}71\) L.
Valore della costante R
Inserendo i valori di riferimento a 0 °C e 1 atm si ottiene:
\[ R = \frac{p_0 V_0}{273^\circ} = \frac{1 \text{ atm} \cdot 22.41 \text{ litri}}{273^\circ} = 0.082 \text{ litri atmosfera/K mole} \]
e, in unità SI:
\[ R = \frac{p_0 V_0}{273^\circ} = \frac{10^5 \text{ pascal} \cdot 22.41 \cdot 10^{-3} \text{ m}^3}{273^\circ} = 8.325 \text{ joule/K mole.} \]
L’incertezza numerica riflette le approssimazioni dei dati di riferimento; il valore attuale in SI è \(R \approx 8{,}314\,462\,618 \,\mathrm{J\,mol^{-1}\,K^{-1}}\), coerente con la definizione esatta della costante di Avogadro nella riforma del SI.
Miscele ideali e legge di Dalton
Per una miscela di gas ideali in un volume V, si definisce pressione parziale del componente i la pressione che esso eserciterebbe se occupasse da solo l’intero volume V alla stessa temperatura. Se \(n_1, n_2, n_3, \dots\) sono le moli dei diversi costituenti, valgono:
\[ p_1 = \frac{n_1}{V} R T, \quad p_2 = \frac{n_2}{V} R T, \quad p_3 = \frac{n_3}{V} R T, \ldots \]
La legge di Dalton stabilisce l’additività delle pressioni parziali:
\[ p = \frac{n}{V} R T = \left( \frac{n_1 + n_2 + n_3 + \ldots}{V} \right) R T = \sum_i \frac{n_i}{V} R T = \sum_i p_i = p_1 + p_2 + p_3 + \ldots \]
È spesso utile introdurre la frazione molare \(x_i = n_i/n\), per cui \(p_i = x_i\,p\). In presenza di vapore saturo, la pressione totale è la somma tra la pressione del vapore saturo e le pressioni parziali degli altri gas. Scostamenti dalla legge di Dalton si osservano quando le interazioni fra componenti non sono trascurabili o vi sono reazioni chimiche in miscela.
Condizioni di riferimento e trasformazioni pratiche
In ambito biologico e tecnico, per confrontare misure eseguite in condizioni diverse, si riportano spesso volumi e pressioni alle condizioni normali di temperatura e pressione (NTP): 0 °C e 1 atmosfera = 760 mmHg. Le leggi dei gas perfetti consentono di trasformare grandezze operative nelle corrispondenti grandezze a NTP:
- Isoterma: \(T\) costante, \(pV = \text{costante}\);
- Isobara: \(p\) costante, \(V \propto T\);
- Isocora: \(V\) costante, \(p \propto T\).
Esempio applicativo: 10,0 L di aria a 25,0 °C e 1,00 atm contengono \(n = \frac{pV}{RT} \approx \frac{1{,}00 \cdot 10{,}0}{0{,}082 \cdot 298} \approx 0{,}41\) mol. Se l’ossigeno rappresenta il 21 % in moli, la sua pressione parziale è \(p_{\mathrm{O_2}} = 0{,}21 \cdot 1{,}00 \,\mathrm{atm} = 0{,}21 \,\mathrm{atm}\).
Interpretazione microscopica e velocità quadratica media
Nel modello cinetico, l’energia interna di un gas ideale dipende solo dalla temperatura. La velocità quadratica media delle molecole è legata a T da:
\[ v_{\mathrm{rms}} = \sqrt{\frac{3 R T}{M}} \]
dove \(M\) è la massa molare del gas. In termini di grandezze microscopiche, la stessa relazione si esprime come \(v_{\mathrm{rms}} = \sqrt{\frac{3k_B T}{m}}\), con \(k_B\) costante di Boltzmann e m massa della singola particella. Un aumento di T comporta un incremento dell’agitazione termica e, quindi, della pressione a volume costante, in accordo con l’equazione di stato. La distribuzione delle velocità è descritta dalla statistica di Maxwell–Boltzmann, coerente con l’ipotesi di urti elastici e assenza di interazioni a lungo raggio.