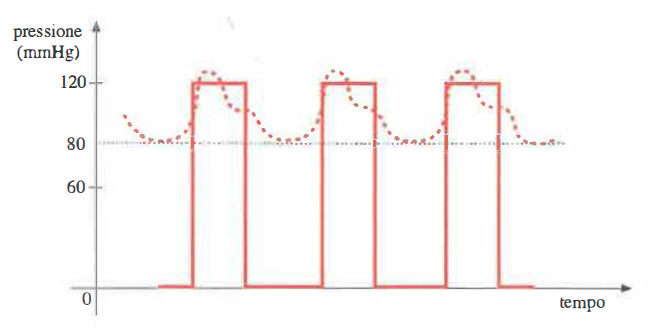
L’effetto idrodinamico cardine della distensibilità dei vasi consiste nel convertire l’alternanza pressoria indotta dal cuore in un regime di flusso quasi continuo. Se le arterie si comportassero come condotti rigidi, la pressione arteriosa precipiterebbe verso lo zero durante l’intervallo in cui la valvola aortica è chiusa, come schematizzato in (Figura 04.05-01). La natura elastica dell’aorta, invece, consente alla parete di espandersi in sistole, assorbendo parte dell’energia meccanica del getto espulso.

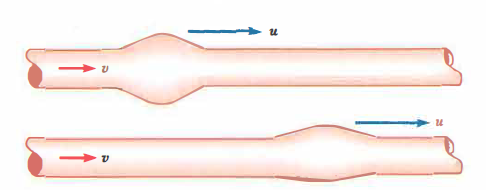
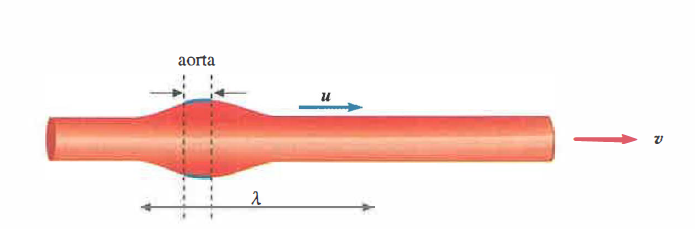
Alla chiusura della valvola aortica, inizia la diastole: la pressione aortica decade gradualmente, senza annullarsi, per l’azione di richiamo della parete, che restituisce l’energia immagazzinata durante la fase di distensione. Da ciò deriva il classico profilo pressorio, oscillante tra un picco sistolico e un minimo diastolico, con successiva risalita quando la valvola si riapre e le pareti si ridistendono. In termini energetici, la distensibilità opera come un serbatoio elastico: durante la sistole parte dell’energia cinetica del sangue viene convertita in energia potenziale elastica nella parete; nella diastole, tale energia viene rilasciata e riconvertita in moto del fluido, contribuendo alla continuità della portata. La dilatazione non è istantanea né omogenea lungo l’albero arterioso: ha origine nell’aorta prossimale e si trasmette progressivamente lungo le grandi arterie come un’onda di deformazione (onda sfigmica) a elevata velocità (Figura 04.05-02).

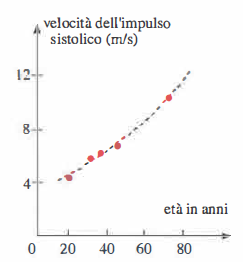
La velocità di propagazione della deformazione della parete, che indichiamo con u, è proprietà del sistema parete-sangue e dipende da parametri geometrici e meccanici (raggio, spessore, modulo elastico, densità del sangue). Per pareti relativamente sottili e comportamento elastico lineare, la velocità u può essere stimata con la relazione di Moens-Korteweg: \( u \approx \sqrt{\frac{E h}{2 \rho R}} \), dove E è il modulo di Young della parete, h lo spessore, R il raggio interno e ρ la densità del sangue. Tale velocità (tipicamente 4–12 m/s nelle grandi arterie); (Figura 04.05-03) è nettamente superiore alla velocità media del sangue v; non va quindi confusa con essa. L’onda di parete impone brevi impulsi di spinta alla massa di fluido, che avanza con velocità media molto più bassa e non “segue” l’onda elastica lungo il vaso. L’aumento di rigidità arteriosa (maggiore E), come avviene con l’invecchiamento o in presenza di arteriosclerosi, incrementa la velocità d’onda e anticipa le riflessioni periferiche, contribuendo all’aumento della pressione sistolica e dell’ampiezza pressoria, fenomeno coerente con quanto descritto in (Figura 04.05-03).

La velocità media del sangue è tuttavia determinata principalmente dalla componente quasi stazionaria del gradiente pressorio. Come suggerito dalla curva tratteggiata in (Figura 04.05-07), la pressione arteriosa può essere scomposta in una quota pressoché costante, dell’ordine di 80 mmHg, e in una componente pulsatile che oscilla tra circa 80 e 120 mmHg. La parte oscillatoria, pur importante per la dinamica locale, fornisce un contributo alla portata media di entità limitata (dell’ordine di qualche decina percentuale), mentre la distensibilità garantisce lo smorzamento delle oscillazioni e la relativa continuità della perfusione.

Il comportamento dei diversi distretti vascolari risponde a ruoli complementari:

• arterie di condotta: elevata cedevolezza relativa e funzione “Windkessel”, con accumulo e rilascio ciclico di energia elastica per stabilizzare pressione e flusso;
• arteriole: regolazione attiva della resistenza idrodinamica attraverso il tono della muscolatura liscia, con modulazione del raggio e quindi delle perdite per attrito;
• sistema venoso: ampia distensibilità e ruolo di serbatoio di volume, tale per cui minime variazioni di pressione transmurale si traducono in rilevanti modifiche del contenuto di volume, contribuendo alla ripartizione e al rientro venoso.

Per interpretare correttamente la (Figura 04.05-04), conviene stimare la lunghezza d’onda associata alla deformazione propagante. Se, a titolo di esempio, si assume u = 6,0 m/s e una frequenza cardiaca ν = 1,1 s⁻¹, dalla relazione \( u = \lambda \, \nu \) segue \( \lambda = u/\nu \approx 5,5 \) m. Poiché la lunghezza dell’aorta è di circa 0,5 m, risulta \( \lambda \gg \) lunghezza del vaso: l’intera aorta si distende e si rilascia quasi all’unisono, configurando l’effetto Windkessel. In (Figura 04.05-04) l’aorta rappresenta dunque una frazione modesta della deformazione d’onda. Superate le approssimazioni elementari, la descrizione si avvicina al comportamento reale del sistema circolatorio (Figura 04.05-05), cui si accede, per maggior dettaglio, attraverso i principi della meccanica applicati al moto non stazionario dei fluidi in condotti deformabili.

Image Gallery

Pressione aortica e ventricolare

La curva tratteggiata rappresenta indicativamente la pressione nell’aorta durante alcuni cicli cardiaci, mentre quella continua schematizza l’andamento della pressione nel ventricolo. Se l’aorta fosse rigida, la pressione arteriosa seguirebbe quella ventricolare. Osserva che la curva tratteggiata si suddivide in due parti: una costante pari a 80 mmHg e una pulsatile fra 80 e 120 mmHg.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Onda sfigmica

La deformazione elastica si pro­paga lungo la parete del vaso (onda sfigmica) ad alta velocità u. Il sangue si muove a velocità v molto inferiore.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Velocità di propagazione ed età

Velocità di propagazione della deformazione elastica lungo le pareti dei vasi all’aumentare dell’età del soggetto. L’aumento di rigidità della parete causa un consistente incremento di velocità nella propagazione della deformazione elastica, cui corrisponde una diminuzione della velocità media del sangue. Per mantenere costante la portata di sangue verso i tessuti è perciò necessario incrementare la pressione fornita dal cuore: da ciò deriva il fenomeno dell’ipertensione nei soggetti anziani.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Velocità di propagazione ed età

Velocità di propagazione della deformazione elastica lungo le pareti dei vasi all’aumentare dell’età del soggetto. L’aumento di rigidità della parete causa un consistente incremento di velocità nella propagazione della deformazione elastica, cui corrisponde una diminuzione della velocità media del sangue. Per mantenere costante la portata di sangue verso i tessuti è perciò necessario incrementare la pressione fornita dal cuore: da ciò deriva il fenomeno dell’ipertensione nei soggetti anziani.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Raggio di equilibrio di un vaso

Metodo grafico per determinare il raggio di equilibrio di un vaso. In presenza di sola tensione elastica passiva, ai due valori della pressione transmurale corrispondono i due raggi di equilibrio Rₑ₁ ed Rₑ₂. L’azione della tensione elastica attiva comporta due posizioni di equilibrio, una stabile, Res, e l’altra instabile, Rei; questa può comportare la chiusura del vaso. Il vaso con la curva tensione–raggio riportata in figura, in generale, ha pareti sufficientemente rigide da non collassare, malgrado la tensione sia nulla fino al raggio R₀.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Deformazione elastica nell’aorta

La deformazione elastica che si propaga lungo la parete dell’aorta ha una dimensione maggiore dell’aorta, la cui lunghezza è rappresentata dal tratto blu. Ne risulta una dilatazione (e poi un rilascio) praticamente contemporanea di tutta la parete dell’aorta. L’onda sfigmica mostrata in figura corrisponde solo a metà lunghezza d’onda λ.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Deformazione elastica nell’aorta

La deformazione elastica che si propaga lungo la parete dell’aorta ha una dimensione maggiore dell’aorta, la cui lunghezza è rappresentata dal tratto blu. Ne risulta una dilatazione (e poi un rilascio) praticamente contemporanea di tutta la parete dell’aorta. L’onda sfigmica mostrata in figura corrisponde solo a metà lunghezza d’onda λ.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Schema logico del sistema cardiovascolare

Schema logico a blocchi della trattazione del sistema cardiovascolare dove sono state eliminate le tre approssimazioni iniziali per arrivare ad una descrizione quanto più vicina possibile alla realtà del moto pulsatile di un liquidoreale e non omogeneo in condotti distensibili.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Per quantificare le considerazioni precedenti, si adotta un modello a parametri concentrati di un condotto distensibile azionato da una cavità elastica. Consideriamo il ventricolo sinistro che espelle sangue nell’aorta, dove il fluido è soggetto all’azione combinata di tre contributi di forza:

1. attrito viscoso in regime laminare, caratterizzato da una resistenza R (cfr. legge di Poiseuille in forma stazionaria);
2. forza elastica di richiamo della cavità, descrivibile con una costante elastica K secondo la legge di Hooke;
3. forzante di pressione generata dalla contrazione ventricolare, che idealizziamo sinusoidale: \( \Delta p(t) = \Delta p_{0} \cos(\omega t) \), con \( \omega = 2\pi \nu \), da cui la forza agente sulla sezione S è \( F_{p}(t) = S \, \Delta p_{0} \cos(\omega t) \). L’assunzione sinusoidale non riproduce il blocco al riflusso imposto dalla valvola aortica, ma risulta utile per cogliere la risposta dinamica del sistema.

Sommando i contributi e applicando il secondo principio della dinamica, \( F_{\text{tot}} = m a \), con accelerazione \( a = \Delta v / \Delta t \) e ricordando che la portata è \( Q = S v \), si ottiene una relazione tra la differenza di pressione applicata e la portata risultante. Essa introduce l’impedenza meccanica Z del sistema, che lega ampiezze e fase di pressione e flusso nel regime pulsatile:

\[Q = S \frac{\Delta x(t)}{\Delta t} = Q(t) = \frac{\Delta p_0}{Z} \cos(\omega t + \phi) = Q_0 \cos(\omega t + \phi),\]

dove l’impedenza Z dipende dai parametri che sintetizzano viscosità, inerzia del fluido e cedevolezza della cavità:

\[Z = \sqrt{R^2 + \left(\frac{m\omega}{S^2} - \frac{K}{V\omega}\right)^2}.\]

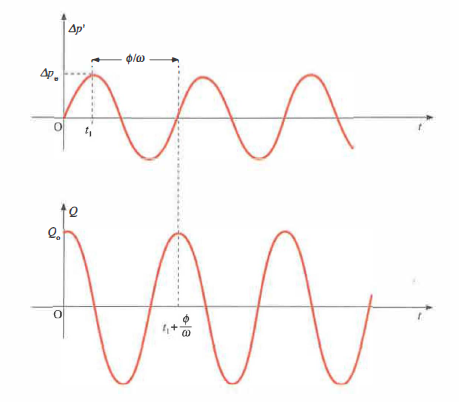
Z ha le dimensioni di una resistenza idraulica e dipende dalla frequenza di eccitazione. Il termine di fase φ nella (8.5) misura lo sfasamento temporale tra variazione di pressione \( \Delta p(t) \) e portata \( Q(t) \), come illustrato in (Figura 04.05-06).

È utile mettere in corrispondenza i parametri con le grandezze “lumped” canoniche. Definiamo l’inerza fluida per unità di sezione \( L = m/S^{2} \) e la compliance della cavità \( C = \Delta V / \Delta p = V/K \). Con tali definizioni, l’espressione reattiva assume la forma standard:

\( Z(\omega) = \sqrt{\, R^{2} + \left( \omega L - \frac{1}{\omega C} \right)^{2} } \),

dove:

• R rappresenta la perdita energetica per attrito viscoso;
• 1/(ωC) è il contributo “capacitivo” associato all’elasticità della parete, che immagazzina e restituisce energia con un ritardo temporale, causando sfasamento tra pressione e flusso;
• ωL è il contributo “induttivo” legato alla massa d’inerzia della colonna fluida.

Per basse frequenze (termine capacitivo dominante), la compliance riduce l’impedenza e la portata tende ad anticipare la pressione; per alte frequenze (inerzia dominante), il flusso tende a ritardare rispetto alla pressione; quando \( \omega L \approx 1/(\omega C) \), i contributi reattivi si compensano e Z si avvicina a R. La frequenza caratteristica \( \omega_{0} \approx 1/\sqrt{L C} \) nei grossi vasi risulta in genere superiore alla frequenza cardiaca, il che spiega perché, nel range fisiologico, resistenza e componente elastica cooperino a smorzare l’ondulazione pur lasciando una quota di sfasamento.

La struttura del profilo di velocità nel flusso pulsatile è ben sintetizzata dal numero di Womersley, \( \alpha = R \sqrt{\omega \rho / \mu} \) (con μ viscosità dinamica). Valori elevati di α, tipici dell’aorta (circa 10–15 a 1–1,5 Hz), indicano profili più piatti e forte dipendenza di fase tra centro e parete; in arterie più piccole, con α dell’ordine di 2–5, i profili si avvicinano a quelli parabolici laminari e l’effetto inerziale è minore. Il quadro, complessivamente, giustifica la capacità del sistema arterioso di convertire un ingresso intermittente in una perfusione periferica relativamente regolare, grazie all’interazione tra resistenza, inerzia e compliance, in accordo con il modello di Windkessel e con le osservazioni sperimentali riportate nelle figure del paragrafo.

Image Gallery

Pressione e portata in condotto rigido

Andamenti temporali della pressione applicata dall’esterno Δp e della conseguente portata Q attraverso il condotto rigido collegato a una cavità distensibile. La portata è sfasata di un angolo φ rispetto alla pressione a causa della massa inerziale del liquido e della distensibilità delle pareti. In generale, ciò significa, per esempio, che il massimo di portata, corrispondente al massimo di compressione avvenuta al tempo t₁, si verifica al tempo t₁ + φ/ω.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.