Fluidi viscosi: moto laminare e moto turbolento
Definizione
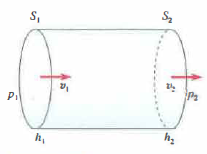
Il teorema di Bernoulli descrive il moto ideale, privo di attriti interni; per i fluidi reali, invece, l’azione dissipativa della viscosità modifica il bilancio energetico. Consideriamo un condotto orizzontale a sezione costante (Figura 03.05-01). Se la velocità risultasse uniforme lungo l’asse, il termine di quota sarebbe costante (h = costante) e, per l’ipotesi ideale, la pressione resterebbe invariata. Nei fluidi reali, però, parte dell’energia meccanica viene convertita in calore per attrito, per cui la relazione di Bernoulli non è più conservativa e la somma delle altezze totali (\[h + \frac{p}{d g} + \frac{v^2}{2 g} = \text{costante}\]) decade lungo il percorso. Indicando con EΛ l’energia dissipata per unità di volume tra le sezioni S₁ e S₂, il bilancio energetico per unità di volume assume la forma seguente, dove d indica la densità del fluido:
\[ d g h_1 + \frac{1}{2} d v_1^2 + p_1 = d g h_2 + \frac{1}{2} d v_2^2 + p_2 + E_\Lambda. \]
Per continuità, in un condotto a sezione costante S₁ = S₂ si ha v₁ = v₂ e, in assetto orizzontale, h₁ = h₂; segue dunque:
\[ E_\Lambda = p_1 - p_2, \]
Ne deriva che, per mantenere un flusso stazionario in un condotto orizzontale reale, è indispensabile una differenza di pressione agli estremi in grado di compensare le perdite viscose. Da ciò discendono due osservazioni utili:
- nel trasporto in condotti rigidi l’energia cinetica gioca un ruolo subordinato rispetto al lavoro compiuto dalle forze di pressione per vincere l’attrito;
- l’azione del peso diventa rilevante solo in presenza di variazioni di quota, come nei tratti verticali, dove la differenza di livello si somma o si oppone alla spinta di pressione.
In generale, per garantire una portata Q in un condotto rigido, occorre imporre una variazione di pressione Δp = p₂ − p₁. Si definisce resistenza idraulica del condotto il rapporto:
\[ R = \frac{\Delta p}{Q} \]
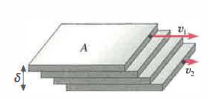
Nei fluidi reali emergono due regimi principali: laminare e turbolento. Nel moto laminare il fluido scorre per lamine adiacenti che slittano l’una rispetto all’altra senza mescolamento macroscopico. In questo caso la forza viscosa tra due lamine, separata distanza δ e di area A, è proporzionale alla velocità relativa v ed è descritta sperimentalmente (Figura 03.05-02) e (Figura 03.05-03) da:
\[ \mathbf{F}_A = -\eta A \frac{v}{\delta} \]
Il coefficiente η è la viscosità dinamica, funzione della natura del fluido e della temperatura; nei liquidi, in genere, diminuisce al crescere di T. Le sue dimensioni sono [M L⁻¹ T⁻¹]. Nel sistema C.G.S. l’unità è il poise (P = g·cm⁻¹·s⁻¹), che corrisponde a 10⁻¹ Pa·s nel SI. Valori tipici per diversi fluidi sono riportati in (Tabella 03.05-01). È spesso utile introdurre anche la viscosità cinematica, \(\nu = \eta/d\), con dimensioni [L² T⁻¹] (unità SI: m²/s).
Per un fluido newtoniano, incomprimibile, in regime stazionario, con profilo sviluppato in un tubo cilindrico di raggio r e lunghezza ℓ, e in assenza di scorrimento sulle pareti, la resistenza idraulica nel regime laminare risulta:
\[ R = \frac{8 \eta \ell}{\pi r^4} \]
Dalle formule si ottiene la nota relazione di Poiseuille tra portata e salto di pressione:
\[ Q = \frac{\pi r^4}{8 \eta \ell} \Delta p \]
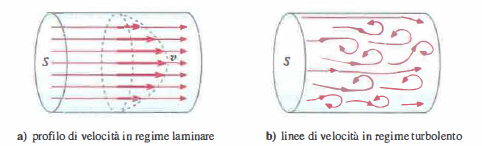
Nel regime laminare la velocità presenta un profilo parabolico (Figura 03.05-03), massimo sull’asse e nullo alla parete per la condizione di non scorrimento; una forma tipica è \(v(\rho) = \frac{\Delta p}{4 \eta \ell}\,(r^2 - \rho^2)\), con \(\rho\) distanza radiale dall’asse. Il profilo nasce dall’equilibrio tra il gradiente di pressione e lo sforzo viscoso, più intenso presso la parete e minore nella regione centrale.
Aumentando progressivamente la differenza di pressione, e quindi la velocità media, si osserva che oltre una certa soglia la legge di Poiseuille non descrive più il comportamento del flusso. La velocità critica può essere espressa come:
\[ v_c = \mathfrak{R} \frac{\eta}{d r} \]
dove \(\mathfrak{R}\) è il numero di Reynolds critico, adimensionale, che per condotti rettilinei e lisci assume valori dell’ordine di 1000÷1200 nella convenzione basata sul raggio. Nella formulazione più diffusa, fondata sul diametro \(D = 2r\), il numero di Reynolds è \( \mathrm{Re} = \dfrac{d\, v\, D}{\eta} \) e la soglia di transizione si colloca tipicamente intorno a 2000÷2300. Il superamento di tale valore porta al regime turbolento, caratterizzato da vortici e intense fluttuazioni che mescolano il fluido tra asse e periferia (Figura 03.05-03). Irregolarità interne, brusche variazioni di sezione, curve e strozzature abbassano sensibilmente il valore critico locale, favorendo l’innesco della turbolenza.
Il cambiamento di regime è brusco e collettivo, con caratteristiche analoghe a una transizione, poiché interessa l’intera sezione non appena è raggiunta la condizione critica. La turbolenza accresce la dissipazione e quindi la resistenza del condotto: i vortici trasportano porzioni di fluido che ruotano rapidamente ma si traslano più lentamente, comportandosi come lamine arrotolate su sé stesse che generano attriti localizzati. In conseguenza di ciò, nel regime turbolento la resistenza cresce con la portata:
\[ R = K Q \]
dove K è un fattore di attrito dipendente dalla geometria e dallo stato superficiale del condotto. Unendo \[R = \frac{\Delta p}{Q}\] e \[R = K Q\], \(R = \Delta p/Q = K Q\), si ottiene una relazione non lineare tra portata e salto di pressione:
\[ Q \propto \sqrt{\Delta p} \]
Ne segue, ad esempio, che raddoppiare la portata in regime turbolento richiede un Δp circa quadruplo, a differenza del caso laminare in cui vale la proporzionalità diretta. Il regime turbolento si accompagna spesso a emissione acustica e vibrazioni, manifestazioni dell’energia dissipata su un ampio spettro di scale.
La legge di Poiseuille si applica sia ai liquidi sia ai gas, purché il fluido sia newtoniano, il flusso sia incomprimibile o debolmente comprimibile e il regime laminare sia pienamente sviluppato. Il teorema di Bernoulli, in forma classica, richiede incomprimibilità e assenza di perdite; per i gas può essere impiegato solo entro variazioni di pressione moderate e, se necessario, integrato con correzioni per la comprimibilità.
Esempi applicativi e note operative
- Esempio laminare: acqua a 20 °C con \(\eta \approx 1,0 \times 10^{-3}\) Pa·s scorre in un capillare di raggio \(r = 1,0 \times 10^{-3}\) m e lunghezza \(\ell = 0,50\) m. Con \(\Delta p = 2,0 \times 10^{3}\) Pa, dalla (6.19) segue \(Q \approx 1,6 \times 10^{-9}\) m³/s. La velocità media è \(v = Q/(\pi r^2) \approx 5,0 \times 10^{-4}\) m/s e, usando il diametro, \(\mathrm{Re} \approx \dfrac{d v (2r)}{\eta} \approx 1\), pienamente laminare;
- Perdita di carico: la variazione di pressione può essere espressa anche come perdita di carico \(\Delta h_f = \Delta p/(d g)\), utile per confrontare effetti di quota e attrito nel bilancio di energia;
- Sensibilità al raggio: la fortissima dipendenza \(Q \propto r^4\) in (6.19) implica che piccole variazioni di r si traducono in grandi modifiche della portata, aspetto cruciale in microfluidica e in emodinamica;
- Rugosità e transizione: superfici interne non lisce aumentano K e abbassano la velocità critica, anticipando la turbolenza anche a Reynolds moderati.
| Fluido | Temperatura (°C) | Viscosità (poise) | Nota |
|---|---|---|---|
| Acqua | 0 | 0.0178 | Parametro di riferimento per fluidi biologici. |
| Acqua | 10 | 0.0130 | La viscosità diminuisce con l’aumento della temperatura. |
| Acqua | 20 | 0.0100 | Valore standard usato come confronto nei laboratori di biochimica. |
| Alcol etilico | 20 | 0.0125 | Fluido con viscosità simile all’acqua, utilizzato come solvente in laboratorio. |
| Etere | 20 | 0.0023 | Estremamente fluido, spesso impiegato in reazioni organiche. |
| Glicerina | 15 | 2.3400 | Altamente viscosa; modello di riferimento per studiare la dinamica dei fluidi densi. |
| Mercurio | 20 | 0.0157 | Metallo liquido, usato come confronto sperimentale per fluidi ad alta densità. |
| Aria | 15 | 0.00018 | Viscosità bassissima, rilevante nei modelli respiratori. |
| Plasma sanguigno | 37 | ~0.012 | Parametro fondamentale per la fluidodinamica circolatoria. |
| Sangue intero | 37 | ~0.035 | La viscosità varia in base all’ematocrito e alla temperatura corporea. |
| Liquor (CSF) | 37 | ~0.010 | Proprietà simili all’acqua, importante nello studio della dinamica craniospinale. |
Viscosità di differenti fluidi
Valori del coefficiente viscoso per vari tipi di liquidi.