Elasticità e legge di Hooke
Definizione
Finora si sono trattati corpi ideali rigidi, privi di deformazioni. In realtà, ogni solido reale si deforma, talvolta in modo minimo, talvolta sensibilmente anche sotto sollecitazioni modeste. Si definisce elastico un corpo che, rimosse le cause della deformazione, recupera la configurazione iniziale; si parla invece di comportamento plastico quando una parte della deformazione permane nel tempo. Per molte sostanze, entro un intervallo limitato di sollecitazioni, la relazione tra sforzo applicato e deformazione risulta pressoché lineare: è il regime di elasticità lineare, pilastro della legge di Hooke e, per estensione, del modello dell’oscillatore elastico che produce moto armonico semplice.
Al di sotto del limite di proporzionalità (e comunque prima del limite elastico), lo sforzo è proporzionale alla deformazione. Il coefficiente di proporzionalità è una costante di materiale che quantifica la rigidezza del corpo nel tipo di sollecitazione considerata.
Sollecitazioni assiali e modulo di Young
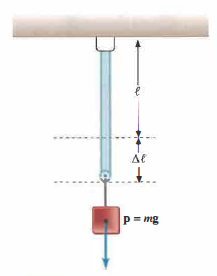
Per un’asta soggetta ad allungamento o compressione uniaxiale (Figura 02.15-01), la legge di Hooke assume la forma classica:
\[ \frac{F}{A} = E \frac{\Delta \ell}{\ell} \]
dove F è il modulo della forza applicata, A l’area della sezione, \(\Delta \ell\) l’allungamento e \(\ell\) la lunghezza iniziale. La costante E è il modulo di Young, con unità di misura Pascal (Pa = N/m²): valori elevati di E corrispondono a materiali più rigidi. Nella (Tabella 02.15-01) sono riportati valori tipici del modulo di Young per diversi materiali e tessuti.
È comune esprimere tali grandezze in termini adimensionali e intensivi: lo sforzo normale (stress) \(\sigma = F/A\) e la deformazione unitaria (strain) \(\varepsilon = \Delta \ell / \ell\). La relazione di proporzionalità diventa quindi:
\[ \sigma = E \varepsilon \]
Deformazioni volumetriche e modulo di compressibilità
Per una sollecitazione idrostatica (compressione uniforme), la legge di Hooke si riformula introducendo il modulo di compressibilità (o di bulk) K, che lega variazione di pressione e variazione relativa di volume:
\[ \Delta p = -K \frac{\Delta V}{V} \]
Qui \(\Delta p\) è la variazione di pressione, V il volume iniziale e \(\Delta V\) la variazione di volume; il segno meno indica che un aumento di pressione produce una diminuzione del volume. Materiali quasi incomprimibili presentano K molto grande; nei fluidi reali K è finito ma elevato.
Membrane sottili: risposta estensionale
Per membrane bidimensionali tese lungo il bordo, la risposta elastica superficiale si descrive mediante:
\[ \frac{F}{\ell} = k \frac{\Delta S}{S} \]
dove \(F/\ell\) è la forza applicata per unità di lunghezza del contorno, S è l’area iniziale della membrana, \(\Delta S\) l’incremento di area e k la costante elastica superficiale (modulo areale), con dimensioni di N/m.
Osservazioni su validità, anisotropia e moduli correlati
Le relazioni sopra esposte valgono nel regime di piccoli spostamenti e deformazioni, per materiali che si comportano linearmente ed in assenza di effetti istantanei non lineari o di isteresi. Oltre il limite elastico compaiono plasticità, danneggiamento o instabilità (p.es., snellezza e instabilità di Euler). Nei materiali isotropi, i moduli elastici fondamentali sono tra loro legati: il modulo di taglio G e il coefficiente di Poisson \(\nu\) soddisfano \( E = 2G(1+\nu) \) e \( K = \frac{E}{3(1-2\nu)} \). Materiali anisotropi (ad esempio compositi stratificati e tessuti biologici) richiedono una descrizione tensoreale più generale, con leggi costitutive direzionali:
- Stress e pressione si misurano in Pascal (Pa), la deformazione unitaria è adimensionale;
- E (modulo di Young) governa allungamenti/compressioni assiali, K la comprimibilità volumetrica, k la risposta estensionale di membrane sottili;
- La linearità è un’approssimazione valida per piccole deformazioni; la sua accuratezza dipende dal materiale e dal livello di sforzo.
Esempio numerico (asta in trazione)
Si consideri un filo di acciaio lungo \(\ell = 2{,}0\) m e sezione \(A = 1{,}0\) mm², sottoposto a trazione \(F = 100\) N. Assumendo \(E \approx 200\) GPa, l’allungamento è \[ \Delta \ell = \frac{F\,\ell}{E\,A} = \frac{100 \cdot 2{,}0}{200 \cdot 10^{9} \cdot 1{,}0 \cdot 10^{-6}} \approx 1{,}0 \times 10^{-3}\ \text{m} = 1{,}0\ \text{mm}. \] Gli sforzi e le deformazioni risultano \(\sigma = F/A \approx 100\ \text{MPa}\) ed \(\varepsilon = \Delta \ell/\ell = 5{,}0 \times 10^{-4}\), compatibili con il regime elastico lineare per acciai strutturali.
| Materiale | E (N/m²) | Nota |
|---|---|---|
| Acciaio | 2 × 10¹¹ | Materiale di riferimento per resistenza, usato come confronto nella biomeccanica ossea. |
| Vetro | 7 × 10¹⁰ | Elevata rigidità, utile come analogia per tessuti fragili. |
| Mattone | 2 × 10¹⁰ | Rigido ma fragile; confronto per materiali ossei in patologie. |
| Ossa (lungo l’asse, trazione) | 1.8 × 10¹⁰ | Resistenza elevata quando sottoposte a forze longitudinali. |
| Ossa (lungo l’asse, compressione) | 0.9 × 10¹⁰ | Minor resistenza alla compressione rispetto alla trazione. |
| Legno duro | 1 × 10¹⁰ | Analogo biomeccanico in studi di protesi e materiali naturali. |
| Tendine | 2 × 10⁷ | Materiale biologico flessibile con alta resistenza alla trazione. |
| Cartilagine (costole) | 1.2 × 10⁷ | Proprietà elastiche fondamentali nella protezione toracica. |
| Gomma | 1 × 10⁶ | Estremamente deformabile, usata come analogia per tessuti molli. |
| Vasi sanguigni | 2 × 10⁵ | Altamente elastici, permettono l’adattamento al flusso ematico. |
| Pelle umana | ~5 × 10⁶ | Buona elasticità, importante per la chirurgia ricostruttiva. |
| Muscolo scheletrico | ~8 × 10⁶ | Elasticità intermedia, varia con lo stato di contrazione. |
| Polmone (parenchima) | ~3 × 10⁵ | Estremamente elastico, rilevante in fisiologia respiratoria. |
Modulo di Young nei materiali e nei tessuti
Valori del modulo elastico in differenti materiali e strutture biologiche.