Quando un fronte d’onda incontra la superficie di separazione tra due mezzi, l’interazione con l’interfaccia può produrre due effetti distinti: una parte dell’onda viene rinviata nel mezzo di provenienza (riflessione), mentre un’altra parte può proseguire nel secondo mezzo con direzione e velocità modificate (rifrazione). Tali comportamenti si deducono in modo elegante dal principio di Huygens, secondo cui ogni punto di un fronte d’onda si comporta come sorgente di onde elementari, la cui inviluppo determina l’evoluzione successiva del fronte stesso.

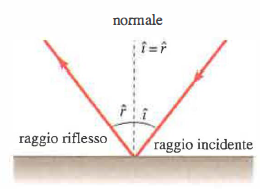
Per la riflessione, le leggi risultanti affermano che il raggio incidente, il raggio riflesso e la normale alla superficie nel punto d’impatto giacciono su uno stesso piano. Inoltre, l’angolo di riflessione \(r\) è uguale all’angolo di incidenza \(i\) (Figura 04.12-01). Questa simmetria angolare è indipendente dalla natura dell’onda (meccanica o elettromagnetica) ed è una conseguenza della reversibilità geometrica del percorso ottico.

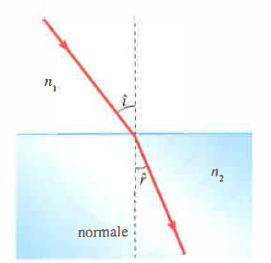
La rifrazione si manifesta quando l’onda penetra in un mezzo con proprietà fisiche differenti, modificando la propria velocità di propagazione. Le leggi di Snell, ricavabili anch’esse dal principio di Huygens, stabiliscono che il raggio incidente, il raggio rifratto e la normale all’interfaccia sono coplanari e che il rapporto tra i seni degli angoli di incidenza \(i\) e di rifrazione \(r'\) è uguale al rapporto tra le velocità di propagazione nei due mezzi. Introducendo gli indici di rifrazione assoluti \(n_{1}\) e \(n_{2}\) (definiti per onde luminose come \(n = c/v\), con \(c\) velocità nel vuoto e \(v\) velocità nel mezzo), si ottiene il coefficiente relativo \(n_{12}\) del secondo mezzo rispetto al primo. La relazione fondamentale è la seguente:

\[ \frac{\text{sen} \, \hat{i}}{\text{sen} \, \hat{r}'} = \frac{v_1}{v_2} = n_{12} = \frac{n_2}{n_1} \]

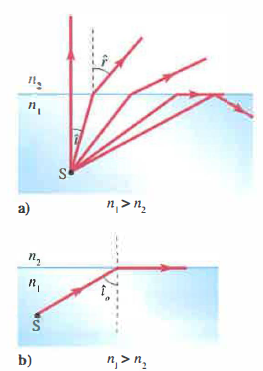
Un’utile interpretazione geometrica discende dal confronto tra le velocità (o, per onde luminose, tra gli indici di rifrazione): se nel secondo mezzo l’onda viaggia più lentamente (\(v_{2} < v_{1}\), cioè \(n_{2} > n_{1}\)), il raggio rifratto si piega verso la normale; se invece la propagazione accelera (\(v_{2} > v_{1}\), cioè \(n_{2} < n_{1}\)), il raggio si allontana dalla normale (Figura 04.12-02). Aumentando l’angolo di incidenza in quest’ultimo caso, si raggiunge una soglia oltre la quale non esiste più un raggio rifratto propagativo: tutta l’energia che non viene assorbita è rinviata nel primo mezzo. Questo è il fenomeno della riflessione totale (Figura 04.12-03), rilevante in molte applicazioni, ad esempio nelle fibre ottiche.

La condizione di riflessione totale richiede che l’onda provenga dal mezzo più rifrangente verso quello meno rifrangente (\(n_{1} > n_{2}\)). L’angolo di incidenza limite \(i_{0}\) è definito dalla situazione in cui il raggio rifratto emergerebbe radente all’interfaccia, cioè con angolo di rifrazione pari a \(90^\circ\). Da Snell si ricava:

\[ \frac{\text{sen} \, \hat{i}_o}{\text{sen} \, 90^\circ} = n_{12}, \quad \text{da cui} \quad \text{sen} \, \hat{i}_o = \frac{n_2}{n_1} \quad (n_1 > n_2). \]

Per le onde elettromagnetiche, e in particolare per la luce, la velocità nel vuoto è massima in natura ed è indicata con \(c \approx 3 \cdot 10^{5}\ \text{km/s}\). L’indice assoluto di rifrazione è definito come \(n = c/v\); nel vuoto si ha \(n = 1\) e per qualunque mezzo materiale l’indice risulta \(n > 1\). In ottica, oltre alla dipendenza dalla composizione del mezzo, \(n\) può variare con la frequenza della radiazione (dispersione), influenzando l’entità della rifrazione per diverse lunghezze d’onda:

• Se \(v_{2} < v_{1}\) (equivalentemente \(n_{2} > n_{1}\)), il raggio rifratto si avvicina alla normale;
• Se \(v_{2} > v_{1}\) (equivalentemente \(n_{2} < n_{1}\)), il raggio rifratto si allontana dalla normale;
• La riflessione totale si verifica solo per passaggio da mezzo più a meno rifrangente, con \(i > i_{0}\) e \(\sin \hat{i}_{0} = n_{2}/n_{1}\).

Esempi numerici distinti: 
1) Incidenza dall’aria a un polimero trasparente: \(n_{1} = 1{,}00\), \(n_{2} = 1{,}49\), \(i = 30^\circ\). Da Snell, \(\sin r' = (n_{1}/n_{2}) \sin i = (1{,}00/1{,}49)\, \sin 30^\circ \approx 0{,}336\), dunque \(r' \approx 19{,}6^\circ\); 
2) Angolo limite acqua-aria: \(n_{1} = 1{,}33\), \(n_{2} = 1{,}00\). \(\sin i_{0} = 1{,}00/1{,}33 \approx 0{,}752\), per cui \(i_{0} \approx 48{,}8^\circ\).

Image Gallery

Riflessione su superficie non piana

Riflessione del raggio di propagazione di un fenomeno ondulato­rio su una superficie non piana.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Rifrazione tra due mezzi

Rifrazione del raggio di propagazione di un fenomeno ondulatorio tra due mezzi di indice di rifrazione n₁ ed n₂ diversi.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Riflessione totale

Il fenomeno della riflessione totale si ha quando il raggio incidente passa da un mezzo a maggior indice di rifrazione (velocità di propagazione minore) a uno con indice di rifrazione minore (velocità di propagazione maggiore).

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.