Vincoli e leve
TOPICS
Definizione
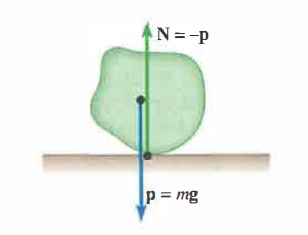
La libertà di movimento di un corpo può essere ridotta dall’azione di vincoli meccanici. Un vincolo fisso ideale è un elemento che, nelle ipotesi del modello, non trasla né si deforma sotto l’azione delle forze applicate e le cui reazioni non compiono lavoro negli spostamenti compatibili. Un esempio elementare è il piano orizzontale che sostiene un corpo: il peso è bilanciato dalla reazione normale del piano, uguale e contraria, e l’equilibrio traslatorio è garantito (Figura 02.12-01). Altri vincoli tipici sono cerniere, perni e assi di rotazione che guidano il moto di pendoli, ruote, eliche e dispositivi analoghi.
In termini di gradi di libertà, un corpo rigido libero nello spazio ha sei gradi di libertà (tre traslazioni e tre rotazioni); l’introduzione di vincoli ne riduce il numero, introducendo reazioni vincolari che si adeguano alle forze esterne per soddisfare le condizioni d’equilibrio. In particolare, se il corpo rigido è incernierato in un punto, la risultante R delle forze può essere sempre assorbita dalla reazione della cerniera. In tal caso, l’equilibrio rispetto alla traslazione è automaticamente assicurato dalla reazione del vincolo, e la condizione necessaria e sufficiente di equilibrio è la sola condizione di equilibrio dei momenti rispetto al punto di attacco del vincolo, cioè la condizione di equilibrio rotazionale.
Se invece il corpo è libero di ruotare attorno a un asse fisso, l’equilibrio è garantito quando la somma vettoriale delle componenti dei momenti delle forze lungo l’asse di rotazione è nulla. In tali contesti risulta utile introdurre il concetto di momento torcente, con unità di misura N·m, calcolato come prodotto della forza per il braccio, ossia la distanza perpendicolare tra la retta d’azione della forza e il punto o l’asse rispetto a cui si valuta il momento.
Leva rigida, principio dei momenti e guadagno meccanico
Una leva è un’asta rigida incernierata a un fulcro, cioè a un asse perpendicolare all’asta, attorno al quale l’asta può ruotare. Consideriamo due forze complanari e perpendicolari all’asse del fulcro: una forza motrice \(F_m\), applicata in un punto M, e una forza resistente \(F_r\), applicata in un punto R (Figura 02.12-02). Indichiamo con \(b_m\) e \(b_r\) i bracci delle rispettive forze, ossia le distanze perpendicolari dei punti M ed R dal fulcro O. La condizione d’equilibrio della leva, in assenza di attriti, richiede l’annullamento del momento risultante rispetto a O:
\[b_m F_m - b_r F_r = 0\]
da cui:
\[ b_m F_m = b_r F_r. \]
Il rapporto adimensionale tra forza resistente e forza motrice,
\[ G = \frac{F_r}{F_m} = \frac{b_m}{b_r}, \]
viene detto guadagno meccanico. In un sistema ideale, un guadagno in forza si accompagna a una perdita in spostamento: per lavoro virtuale nullo delle reazioni, la conservazione del lavoro implica \(F_m\,\Delta s_m \approx F_r\,\Delta s_r\), con \(\Delta s_m/\Delta s_r \approx b_r/b_m\).
Classi di leve e vantaggio meccanico
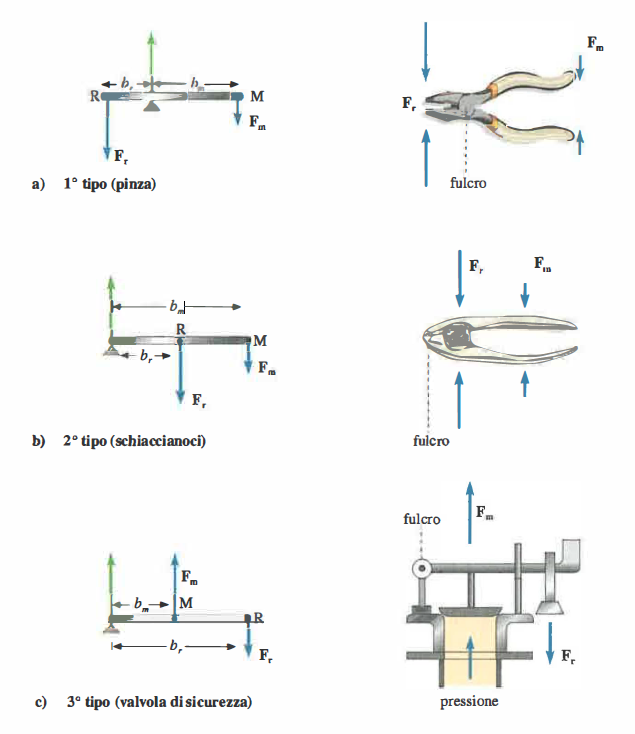
La classificazione canonica distingue tre configurazioni, a seconda della posizione del fulcro rispetto ai punti di applicazione delle forze (Figura 02.12-02):
- Leve di primo genere (Figura 02.12-02), con fulcro interposto tra M ed R: il guadagno può essere maggiore, uguale o minore di 1 a seconda del rapporto \(b_m/b_r\); esempi: la stadera a due bracci, le forbici da carta;
- Leve di secondo genere (Figura 02.12-02), con R tra fulcro e M: il guadagno è sempre maggiore di 1, poiché \(b_m > b_r\); esempi: l’apribottiglie a leva, il tagliabulloni;
- Leve di terzo genere (Figura 02.12-02), con M tra fulcro ed R: il guadagno è sempre minore di 1; esempi: le pinzette, il sistema avambraccio–bicipite nell’alzare un carico.
La disposizione di (Figura 02.12-02) è anche interpretabile come una leva di primo genere a bracci uguali, utile per discutere il ruolo dei dispositivi di rinvio. Più in generale, la scelta della classe deriva dal compito: massimizzare la forza (secondo genere) o la rapidità/spostamento del punto resistente (terzo genere), con il primo genere che consente di variare la direzione della forza e di modulare il guadagno.
Carrucole, pulegge e modelli ideali
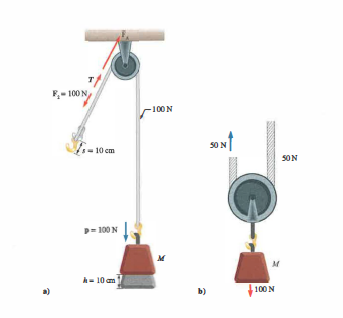
Nel lessico tecnico, “carrucola” indica una macchina semplice impiegata per sollevare carichi mediante una fune, mentre “puleggia” è l’organo di trasmissione costituito da un disco che ruota attorno al proprio asse, ad esempio per cinghie e catene. Un sistema di rinvio fisso con fune inestensibile e priva di massa è equivalente a una leva di primo genere a bracci uguali: in condizioni ideali, la forza motrice F che si applica all’estremità libera della fune e la forza resistente p che agisce sul carico hanno modulo uguale, e il guadagno è pari a 1. In presenza di peso della fune e attrito tra gola della puleggia e fune, la tensione non è uniforme e la forza richiesta supera il carico, per cui il guadagno effettivo diventa minore di 1.
Configurazioni con carrucole mobili, come in (Figura 02.12-03) , permettono di amplificare il modulo della forza a parità di lavoro: una carrucola mobile ideale raddoppia la tensione agente sul carico, fornendo un guadagno teorico \(G \approx 2\); sistemi a più rinvii (paranchi) consentono guadagni anche superiori, a scapito dello spostamento che la mano deve compiere e delle perdite per attrito.
Osservazioni operative e criteri di calcolo
- Il momento di una forza rispetto a un punto o a un asse si calcola come prodotto forza–braccio, con segno positivo o negativo a seconda del verso di rotazione indotto;
- Nel caso di corpo vincolato in un solo punto, la reazione del vincolo può bilanciare qualsiasi risultante delle forze, rendendo sufficiente la sola condizione sui momenti;
- Per un corpo che ruota attorno a un asse fisso, è necessario e sufficiente annullare la somma delle componenti dei momenti lungo l’asse;
- Le ipotesi ideali (rigidità dei corpi, assenza di attrito, masse trascurabili) sono utili per il progetto preliminare; in esercizi applicativi si introducono coefficienti di attrito e pesi propri per stimare il guadagno reale.
Image Gallery
Image Gallery
Image Gallery
Image Gallery
Image Gallery
Image Gallery
Image Gallery
Image Gallery
