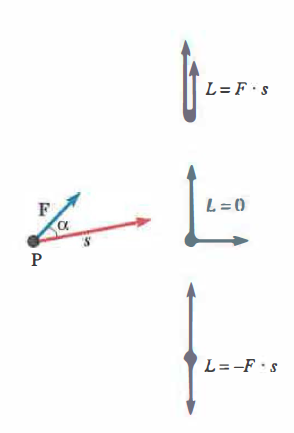
In meccanica classica i concetti di lavoro ed energia costituiscono strumenti unificanti che consentono di analizzare con efficacia un’ampia gamma di problemi. Si dice che una forza compie lavoro quando il suo punto di applicazione subisce uno spostamento. Se la forza, di modulo F, è costante in modulo, direzione e verso, e il punto di applicazione P si sposta di un segmento rettilineo s formando un angolo α con la direzione della forza, il lavoro L svolto da F è definito come prodotto scalare tra forza e spostamento:

\[ L = \mathbf{F} \cdot \mathbf{s} = F\,s\,\cos \alpha \]

Dalla formula segue immediatamente che il lavoro è positivo (lavoro motore) se l’angolo α è acuto, negativo (lavoro resistente) se α è ottuso. Il lavoro risulta massimo quando lo spostamento ha la stessa direzione e verso della forza e nullo quando lo spostamento è ortogonale alla forza (si veda la (Figura 02.09-01). Quest’ultimo caso spiega, ad esempio, perché la forza centripeta in un moto circolare uniforme non compie lavoro.

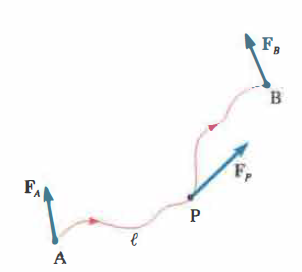
Nel caso generale, quando la forza varia da punto a punto oppure lo spostamento avviene lungo una traiettoria curva, il lavoro compiuto da A a B lungo il cammino Γ è definito come somma dei lavori elementari lungo tratti infinitesimi in cui la forza può considerarsi costante (Figura 02.09-02). In termini analitici, tale somma è il seguente integrale di linea:

\[ L_{A\to B} = \int_{\Gamma} \mathbf{F}\cdot d\mathbf{s}. \]

Nel Sistema Internazionale (SI) l’unità di misura del lavoro è il joule (J), pari al lavoro compiuto da una forza di 1 newton quando il punto di applicazione si sposta di 1 metro nella direzione della forza: 1 J = 1 N·m. Nel sistema C.G.S. si utilizza l’erg: 1 erg = 1 dyn·cm, con la conversione 1 J = 10^{7} erg. In ambito tecnico è storicamente impiegato anche il chilogrammo-forza metro (kgf·m), definito come il lavoro esercitato da 1 kgf lungo 1 m; per la conversione vale approssimativamente 1 J ≈ 0,10197 kgf·m (ossia 1 kgf·m ≈ 9,80665 J), talvolta approssimato come 1/9,8 kgf·m. Su scala atomica e subatomica si adotta l’elettronvolt (eV), pari al lavoro compiuto dalla forza elettrica quando una carica elementare e attraversa una differenza di potenziale di 1 V: 1 eV = 1,602·10^{-19} J.

Con energia di un corpo o di un sistema si intende la sua capacità di compiere lavoro. Lavoro ed energia sono grandezze omogenee e condividono la medesima unità di misura. In natura si incontrano molteplici forme di energia:

• energia cinetica, associata al moto di un corpo;
• energia potenziale gravitazionale, dovuta all’interazione con il campo gravitazionale;
• energia potenziale elettrica e magnetica, connessa ai campi elettromagnetici;
• energia termica (calore), legata all’energia interna e all’agitazione microscopica;
• energia chimica, immagazzinata nei legami molecolari.

Un corpo di massa m in moto con velocità v possiede energia cinetica e, per arrestarlo, occorre compiere un lavoro meccanico che sottragga tale energia; viceversa, una massa sospesa in un campo gravitazionale detiene energia potenziale che, lasciata libera, può convertirsi in energia cinetica e quindi in lavoro o calore per effetto di interazioni dissipative. Le trasformazioni tra diverse forme di energia sono regolate dal principio di conservazione dell’energia, secondo cui, in ogni processo fisico, l’energia totale rimane costante, pur potendo mutare forma (lavoro meccanico incluso). Tale principio vale anche in ambito nucleare, a condizione di includere l’equivalenza massa–energia espressa dalla relazione di Einstein

\[ E = m c^{2}, \]

dove c è la velocità della luce nel vuoto. A seconda del contesto fisico, il principio assume formulazioni specifiche: in meccanica si parlerà di conservazione dell’energia meccanica; in fluidodinamica si incontra il teorema di Bernoulli; in termodinamica il primo principio stabilisce l’equivalenza tra lavoro e trasferimenti di calore.

Image Gallery

Lavoro di una forza costante

Il lavoro compiuto da una forza che rimane costante in modulo, direzione e verso durante il suo spostamento.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Lavoro di una forza variabile

Esempio di una forza che cambia in modulo, direzione e verso nel corso del suo spostamento.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

La quantità di energia cinetica di un punto materiale di massa m che si muove con velocità v, indicata con E_k, è legata a massa e modulo della velocità dalla relazione:

\[ E_{k} = \frac{1}{2}\, m\, v^{2}. \]

Consideriamo ora un punto materiale di massa m inizialmente fermo. Sia applicata una forza risultante costante F, di modulo, direzione e verso fissati. Il moto avviene lungo la direzione di F con accelerazione costante a = F/m; di conseguenza la velocità aumenta e cresce l’energia cinetica. Per coerenza con il principio di conservazione dell’energia, la variazione di energia cinetica del corpo deve eguagliare il lavoro compiuto dalla forza risultante (inclusi eventuali contributi resistivi, come l’attrito, che forniscono lavoro negativo):

\[ L \, (\text{lavoro della forza } \mathbf{F}) = \Delta E_{k} \, (\text{variazione di energia cinetica}). \]

L’uguaglianza è nota come teorema lavoro-energia (o teorema dell’energia cinetica) ed è una conseguenza della seconda legge della dinamica congiunta alla definizione di energia cinetica. Forniamo una dimostrazione nel caso di moto rettilineo uniformemente accelerato. Su un intervallo temporale piccolo Δt vale:

\[ m \frac{\Delta v}{\Delta t} = m \frac{v_{2} - v_{1}}{\Delta t}. \]

Lo spazio percorso in Δt è s = \(\frac{v_{1} + v_{2}}{2}\) Δt, essendo \(\frac{v_{1} + v_{2}}{2}\) la velocità media nell’intervallo. Il lavoro svolto dalla forza F in Δt risulta allora:

\[
L = F \cdot s = ma \cdot s = m \frac{v_2 - v_1}{\Delta t} \cdot \frac{v_2 + v_1}{2} \Delta t 
= \frac{1}{2} m (v_2^2 - v_1^2) = \frac{1}{2} m v_2^2 - \frac{1}{2} m v_1^2 
= E_{K2} - E_{K1} = \Delta E_K
\]

La catena di uguaglianze utilizza la seconda legge di Newton e la definizione di energia cinetica. La conclusione è generale: il lavoro totale delle forze agenti su un punto materiale coincide con la variazione della sua energia cinetica. Infatti, per forze e traiettorie variabili, passando al limite si ottiene la forma integrale

\[ L_{A\to B}=\int_{\Gamma} \mathbf{F}\cdot d\mathbf{s} = \Delta\!\left(\tfrac{1}{2} m v^{2}\right), \]

da cui discende che un lavoro positivo incrementa l’energia cinetica, mentre un lavoro negativo la riduce. Questa formulazione verrà impiegata, a seconda dei casi, insieme a vincoli, attriti e forze conservative, collegando opportunamente lavoro ed energia potenziale.

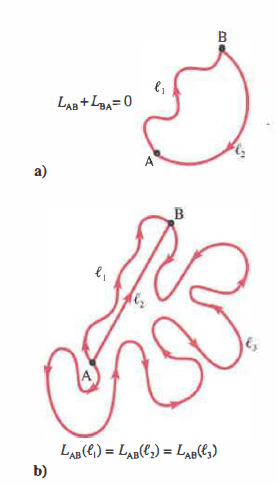
Il lavoro associato a una forza lungo uno spostamento compiuto da un punto A a un punto B, in generale, può dipendere dal tracciato seguito. Si definiscono invece conservative quelle forze per le quali il lavoro dipende esclusivamente dagli estremi del percorso e non dalla traiettoria. In modo equivalente, una forza è conservativa se e solo se il lavoro compiuto lungo qualunque cammino chiuso è nullo (Figura 02.09-03). Se il lavoro lungo una curva chiusa non si annulla, la forza si dice dissipativa.

Queste definizioni si collegano direttamente al teorema dell’energia cinetica: quando il lavoro totale lungo un percorso chiuso è nullo, la variazione di energia cinetica su tale percorso è nulla, mentre in presenza di forze dissipative la variazione di energia cinetica lungo una traiettoria chiusa non è in generale nulla. In simboli, indicando con ΔEk la variazione di energia cinetica, in un campo conservativo vale ΔEk = 0, mentre in presenza di dissipazione si ha tipicamente ΔEk ≠ 0.

Per un campo conservativo, essendo il lavoro tra A e B funzione soltanto degli estremi A(xA, yA, zA) e B(xB, yB, zB), si può introdurre una funzione scalare U(x, y, z), detta energia potenziale, tale che il lavoro sia rappresentabile come salto finito di U tra i due punti:

\[ L_{AB} = U(A) - U(B) \]

L’esistenza di U consente di scrivere localmente la forza come gradiente del potenziale, con segno negativo: \(\mathbf{F} = -\nabla U\). In domini semplicemente connessi, la condizione \(\nabla \times \mathbf{F} = \mathbf{0}\) è necessaria e sufficiente perché la forza sia conservativa, ed è equivalente alla condizione di indipendenza dal percorso del lavoro.

Riprendendo il teorema dell’energia cinetica (relazione \[L \, (\text{lavoro della forza } \mathbf{F}) = \Delta E_{k} \, (\text{variazione di energia cinetica})\]), se tutte le forze agenti sono conservative, allora il lavoro tra una posizione 1 e una posizione 2 è dato dalla differenza di potenziale, e dunque:

\[ \Delta E_{k} = E_{k2} - E_{k1} = L_{12} = U_{1} - U_{2} \]

Da cui segue la costanza della somma tra energia cinetica ed energia potenziale:

\[ U + E_{k} = \text{costante} \]

Questa è la forma compatta del principio di conservazione dell’energia meccanica.

È utile raccogliere alcune proprietà ed esempi:

• Proprietà equivalenti per forze conservative: il lavoro lungo qualsiasi circuito chiuso è nullo; esiste un potenziale scalare U tale che \(\mathbf{F} = -\nabla U\); la circuitazione \(\oint \mathbf{F}\cdot d\mathbf{s} = 0\);
• Esempi di campi conservativi: campi radiali a legge dell’inverso del quadrato (gravitazionale newtoniano, elettrico di cariche puntiformi); campi uniformi (ad esempio il campo gravitazionale vicino alla superficie terrestre); forze elastiche ideali di Hooke;
• Esempi di forze dissipative: attrito radente e viscoso; in questi casi il lavoro su un ciclo è negativo e l’energia meccanica diminuisce convertendosi in calore.

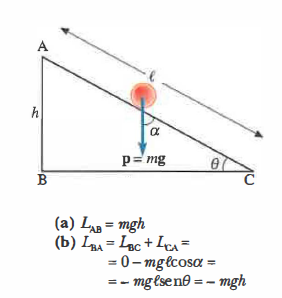
Verifichiamo ora, in prossimità del suolo, la natura conservativa del campo gravitazionale e la forma del potenziale. Consideriamo una massa m che si muove lungo una traiettoria verticale tra un punto A a quota h e il suolo B a quota h = 0, e poi ritorna da B ad A (Figura 02.09-04). Assumendo g costante e lo spostamento orientato verso l’alto:

LAB = +mgh e LBA = −mgh.

La somma lungo il circuito A→B→A è nulla, come richiesto per un campo conservativo. In tali condizioni l’energia potenziale gravitazionale dipende solo dalla quota h del punto rispetto a un riferimento scelto, ed è descritta da:

\[ U = m g h + \text{costante} \]

La costante fissa il livello zero di U e può essere scelta convenientemente; per esempio, ponendo U = 0 alla quota h = 0, si ottiene U = mgh. La scelta dello zero di potenziale non ha effetti sulle differenze di energia, né quindi sulla dinamica.

Un’applicazione tipica del principio (\[U + E_{k} = \text{costante}\]) in campo gravitazionale uniforme è riassunta dalla relazione:

\[ E_k + U = \frac{1}{2}mv^2 + mgh = \text{costante} \]

Esempio didattico alternativo: un blocco scivola senza attrito su un binario che lo porta da una quota h1 a una quota h2. Trascurando attriti, la relazione (\[E_k + U = \frac{1}{2}mv^2 + mgh = \text{costante}\]) fornisce \(\tfrac{1}{2} m v_2^2 + m g h_2 = \tfrac{1}{2} m v_1^2 + m g h_1\). Se il blocco parte da fermo a h1 e scende fino a h2 più basso, la variazione di quota si converte integralmente in energia cinetica. Un’analoga trasformazione, ma in senso opposto, avviene risalendo.

Per le forze elastiche ideali, descritte dalla legge di Hooke F = −kx, l’energia potenziale associata è

\[ U = \frac{1}{2}kx^2 \]

dove x è l’allungamento rispetto alla posizione di equilibrio. Anche in questo caso vale \(\mathbf{F} = -\frac{dU}{dx}\,\hat{\mathbf{x}}\), e l’energia meccanica si conserva in assenza di perdite.

Image Gallery

Campo di forze conservative

Illustrazione grafica delle proprietà di un campo di forze conservative. Le due definizioni di forza conservativa sono equivalenti. Nel caso (b), per andare dal punto A al punto B lungo le traiettorie ℓ₁, ℓ₂ e ℓ₃ se il campo di forze è conservativo avremo: LAB (ℓ₁)  = LAB (ℓ₂) = LAB (ℓ₃)

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Lavoro della forza peso

Il lavoro resistente  LBA della forza peso è uguale quando è calcolato (a) lungo la verticale o (b) lungo il piano inclinato (se lo spostamento è orizzontale rispetto al suolo, essendo la forza peso verticale, il lavoro è nullo per definizione).

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Oltre al lavoro compiuto, è spesso rilevante il tempo necessario per compierlo. Si definisce potenza il rapporto tra il lavoro e l’intervallo temporale in cui viene eseguito:

\[ W = \frac{L}{\Delta t} \]

Nel limite istantaneo, \(W = \frac{dL}{dt}\). Poiché \(L = \int \mathbf{F}\cdot d\mathbf{s}\), si ottiene la ben nota espressione della potenza istantanea come prodotto scalare tra forza e velocità:

\[ W = \frac{L}{\Delta t} = \frac{\mathbf{F} \cdot \Delta s}{\Delta t} = \mathbf{F} \cdot \frac{\Delta s}{\Delta t} = \mathbf{F} \cdot v \] Per evitare ambiguità con il simbolo del watt, molte trattazioni indicano la potenza con P; qui manteniamo W per coerenza con le formule numerate.

Unità di misura: nel Sistema Internazionale la potenza si misura in watt (W), con 1 W = 1 J/s; nel sistema C.G.S. si usa l’erg/s. Sono in uso anche unità pratiche: il chilogrammo-metro al secondo (kg·m/s) e il cavallo vapore (hp), definito come 1 hp = 75 kg·m/s = 75 · 9,8 J/s ≈ 735 W.

Si definisce rendimento il rapporto tra il lavoro utile fornito da una macchina e l’energia totale Ei immessa:

\[ \eta = \frac{L}{E_i} \quad \text{che in percentuale diventa} \quad \eta = \frac{L}{E_i} \cdot 100\% \]

Per conservazione dell’energia si ha sempre \(L \leq E_i\); in assenza di perdite (attriti, turbolenze, dissipazioni elettriche) si avrebbe idealmente \(\eta = 1\) (100%).

Esempio numerico: un argano elettrico assorbe 1,50 kJ per sollevare lentamente un carico di 10,0 kg di un dislivello di 8,0 m. Il lavoro utile è \(L = m g h = 10,0 \cdot 9,8 \cdot 8,0 = 784\ \text{J}\). Il rendimento è \(\eta = 784 / 1500 \approx 0,522\), cioè circa il 52,2%. La differenza \(E_i - L\) è l’energia dissipata, in gran parte sotto forma di calore negli organi meccanici e nei circuiti elettrici.