Un corpo è in moto quando la sua posizione varia nel tempo rispetto a uno o più corpi assunti come fissi, ossia rispetto a un sistema di riferimento. Il moto ha dunque natura intrinsecamente relativa. Nella Meccanica classica, la descrizione completa del movimento si ottiene specificando, per ogni istante, la posizione del corpo nello spazio. A tal fine si fissa un sistema di assi (tipicamente cartesiano) e si introducono le funzioni temporali che forniscono le coordinate del punto. Per caratterizzare lo stato di moto e poter collegare la cinematica alla dinamica, risultano essenziali le grandezze velocità e accelerazione, le quali compaiono direttamente nelle leggi del moto e, in particolare, nella seconda legge di Newton.

Si definisce traiettoria la curva geometrica descritta dal punto durante il suo movimento. Se la traiettoria è nota, la descrizione del moto risulta completa specificando, istante per istante, la posizione lungo tale curva. Indicando con s la lunghezza d’arco percorsa dal punto P in funzione del tempo t, la relazione s = s(t) è detta legge oraria e consente di ricostruire l’evoluzione del moto lungo il percorso assegnato (Figura 02.02-01).

Se la traiettoria non è determinata a priori, occorre fornire la posizione nello spazio in ogni istante. È sufficiente allora conoscere le tre coordinate del punto P rispetto a un sistema cartesiano fisso, cioè le funzioni tempo-dipendenti:

\[ x = x(t), \quad y = y(t), \quad z = z(t) \]

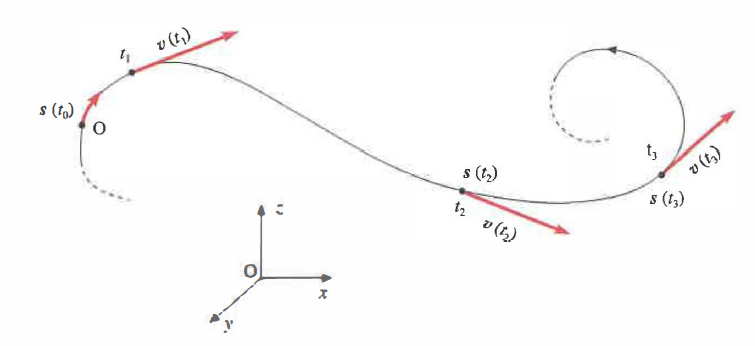
Tali funzioni costituiscono la rappresentazione parametrica della curva spaziale (la traiettoria), con il tempo t come parametro. In altre parole, la legge oraria in forma vettoriale contiene sia l’informazione sulla forma del percorso, sia quella sull’evoluzione temporale lungo di esso. Indicando con \(\mathbf{r}(t) = x(t)\,\mathbf{i} + y(t)\,\mathbf{j} + z(t)\,\mathbf{k}\) il vettore di posizione, si distinguono chiaramente due quantità: la lunghezza d’arco s(t), che è una grandezza scalare crescente con il cammino percorso, e lo spostamento \(\Delta \mathbf{r} = \mathbf{r}(t_2) - \mathbf{r}(t_1)\), che è una grandezza vettoriale e segue le regole del calcolo vettoriale. La distinzione tra s e \(\Delta \mathbf{r}\) è fondamentale quando si confrontano velocità scalare e velocità vettoriale.

Image Gallery

Vettore velocità 3D

Vettore velocità considerato in diversi istanti lungo la traiettoria di moto di un punto. La traiettoria si svolge nelle tre dimensioni.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

La velocità scalare media nell’intervallo temporale \(\Delta t = t_{2} - t_{1}\) è definita da:

\[ v_{m} = \frac{s(t_{2}) - s(t_{1})}{t_{2} - t_{1}} = \frac{\Delta s}{\Delta t} \]

La velocità istantanea è il limite della velocità media per intervalli temporali sempre più piccoli. In termini vettoriali, la velocità \(\mathbf{v}\) è tangente alla traiettoria nel punto considerato, ha verso concorde con l’aumento di s e modulo uguale alla derivata temporale della lunghezza d’arco. In forma vettoriale si scrive:

\[ v_{\text{m}} = \frac{\Delta s}{\Delta t}, \quad v = \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t} \]

dove \(\Delta \mathbf{r}\) è lo spostamento. Nel Sistema Internazionale (S.I.) il modulo della velocità si misura in m s⁻¹; nel sistema C.G.S. in cm s⁻¹.

In modo del tutto analogo, l’accelerazione media è il vettore:

\[ \mathbf{a}_{m} = \frac{\mathbf{v}(t_{2}) - \mathbf{v}(t_{1})}{t_{2} - t_{1}} = \frac{\Delta \mathbf{v}}{\Delta t} \]

e l’accelerazione istantanea è definita da:

\[ a = \lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} \]

Nel S.I. l’accelerazione si misura in m s⁻², nel sistema C.G.S. in cm s⁻². Se la direzione della velocità resta costante nel tempo (moto rettilineo), \(\mathbf{a}\) è allineata con \(\mathbf{v}\). Nei moti curvilinei, invece, l’accelerazione in generale non è tangente alla traiettoria: si decompone in una componente tangenziale, associata alla variazione del modulo di \(\mathbf{v}\), e in una componente normale (o centripeta), legata alla variazione della direzione di \(\mathbf{v}\). In termini locali lungo la traiettoria:

\[ \mathbf{a} = \underbrace{\frac{dv}{dt}\,\hat{\mathbf{t}}}_{a_{t}} + \underbrace{\frac{v^{2}}{\rho}\,\hat{\mathbf{n}}}_{a_{n}}, \]

dove \(\hat{\mathbf{t}}\) è il versore tangente, \(\hat{\mathbf{n}}\) il versore normale verso il centro di curvatura e \(\rho\) il raggio di curvatura del percorso.

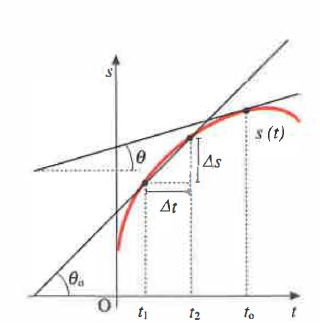
Interpretazione grafica. Consideriamo per semplicità un moto monodimensionale descritto da s = s(t). Il grafico s–t non va confuso con la traiettoria: rappresenta l’evoluzione temporale della distanza percorsa lungo il cammino assegnato. Come mostrato schematicamente in (Figura 02.02-02), la velocità scalare media coincide con il rapporto incrementale di s(t) tra t₁ e t₂, mentre la velocità scalare istantanea è la pendenza della tangente alla curva s(t) nell’istante considerato.

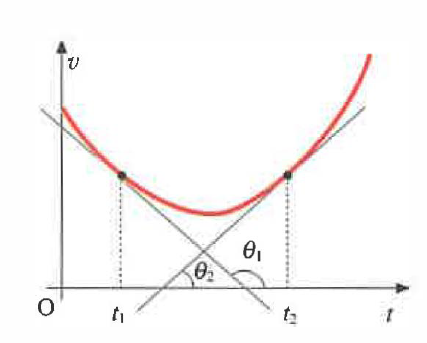
In modo analogo, la funzione v(t) descrive il modulo della velocità nel tempo. Poiché le definizioni di accelerazione si riferiscono al vettore \(\mathbf{v}\), nei moti rettilinei, dove la direzione è fissa, l’accelerazione media risulta il rapporto incrementale di v(t) e quella istantanea la pendenza della curva v–t nell’istante dato (Figura 02.02-03). Se il moto è curvilineo, la pendenza di v(t) fornisce soltanto la componente tangenziale \(a_t = dv/dt\); la componente normale \(a_n\) è connessa alla curvatura della traiettoria ed esprime la variazione di direzione di \(\mathbf{v}\).

Esempio numerico. Un punto materiale si muove lungo un arco di circonferenza di raggio \(\rho = 50,0\) m. Il modulo della velocità cresce linearmente da 0 a 10,0 m s⁻¹ nei primi 10,0 s, cioè v(t) = 1,00 t (con t in s). Tra t₁ = 2,00 s e t₂ = 6,00 s la velocità scalare media vale: \[ v_m = \frac{s(t_2)-s(t_1)}{t_2-t_1} = \frac{\int_{2,00}^{6,00} v(t)\,dt}{4,00} = \frac{\int_{2,00}^{6,00} 1,00 t\,dt}{4,00} = \frac{(t^2/2)_{2,00}^{6,00}}{4,00} = \frac{(36,0-4,00)/2}{4,00} = \frac{16,0}{4,00} = 4,00\ \text{m s}^{-1}. \] All’istante t = 6,00 s si ha v = 6,00 m s⁻¹ e \(dv/dt = 1,00\) m s⁻², quindi: \[ a_t = 1,00\ \text{m s}^{-2}, \quad a_n = \frac{v^2}{\rho} = \frac{(6,00)^2}{50,0} = 0,72\ \text{m s}^{-2}. \] L’accelerazione totale vale \(\sqrt{a_t^2 + a_n^2} \approx 1,24\) m s⁻² ed è inclinata rispetto alla tangente in modo da puntare verso il centro di curvatura:

• Il moto è relativo al sistema di riferimento scelto;
• La legge oraria può essere espressa come s = s(t) lungo una traiettoria nota, oppure come \(\mathbf{r}(t)\) in tre dimensioni;
• La velocità vettoriale è tangente al percorso e si ottiene come derivata di \(\mathbf{r}(t)\);
• L’accelerazione si decompone in parte tangenziale \(dv/dt\) e parte normale \(v^{2}/\rho\);
• Nei grafici s–t e v–t, le pendenze locali rappresentano rispettivamente la velocità scalare e l’accelerazione tangenziale.

Image Gallery

Diagramma spazio-tempo

Diagramma spazio-tempo di un moto. Il rapporto incrementale Δs/Δt = tg θ rappresenta la velocità scalare media. La pendenza della tangente geometrica nel punto t₀ rappresenta la velocità scalare istantanea a t₀:

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Diagramma velocità-tempo

Diagramma velocità-tempo di un moto. La pendenza della curva rappresenta la componente dell'accelerazione nella direzione della velocità (componente tangenziale dell'accelerazione). In t₁ l'accelerazione è negativa, mentre in t₂ è positiva.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Si analizzano ora, dal punto di vista puramente cinematico, alcuni casi paradigmatici di moto.

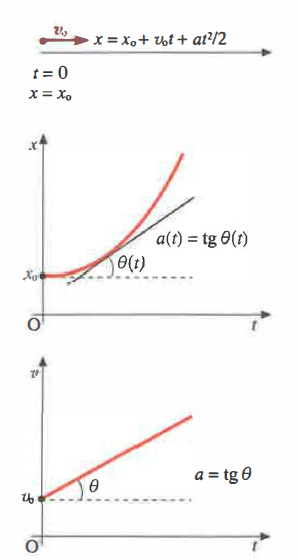
Moto rettilineo uniforme. Quando il vettore velocità \(\mathbf{v}\) rimane costante in modulo, direzione e verso, la traiettoria è una retta che, per comodità, si assume coincidere con l’asse \(x\). Il moto è dunque monodimensionale. Poiché \(\mathbf{v}\) è costante, dalla definizione di velocità come derivata dello spostamento segue che la funzione \(x(t)\) ha pendenza costante. Il diagramma spazio-tempo è pertanto una retta, e la legge oraria è lineare nel tempo:

\[
x = x_{0} + v_{0} t
\]

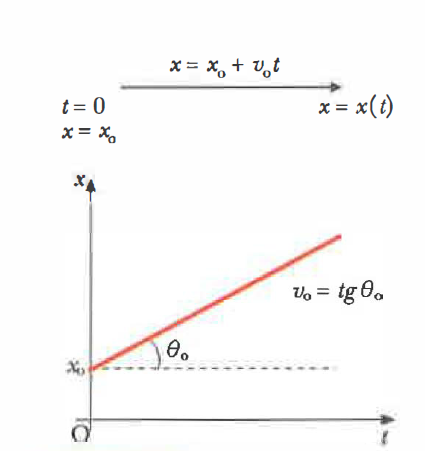
dove \(x_{0}\) è la posizione all’istante \(t = 0\) e \(v_{0}\) è la velocità costante (Figura 02.02-04). L’interpretazione geometrica è immediata: la pendenza del grafico vale \(v_{0}\); se \(v_{0} < 0\), la retta decresce. Le grandezze hanno unità SI: \([x] = \mathrm{m}\), \([v_{0}] = \mathrm{m\,s^{-1}}\), \([t] = \mathrm{s}\).

Moto rettilineo uniformemente accelerato. Se un punto materiale è soggetto a un’accelerazione costante \(\mathbf{a}\), e la velocità iniziale è parallela ad \(\mathbf{a}\) (o nulla), il moto rimane rettilineo e unidimensionale. Il grafico velocità-tempo è una retta di pendenza costante, da cui discende in forma generale:

\[
v = v_{0} + a t
\]

dove \(v_{0}\) è la velocità iniziale e \(a\) è il modulo dell’accelerazione costante. Poiché la pendenza della legge oraria \(x(t)\) è la velocità, la forma di \(x(t)\) è parabolica (Figura 02.02-05):

\[
x = x_{0} + v_{0} t + \frac{1}{2} a t^{2}
\]

Il segno di \(a\) determina l’allungamento o la concavità della parabola (accelerazione concorde o discorde rispetto al verso di \(x\)).

Esempio sintetico (coerente con le relazioni precedenti): un carrello su guida rettilinea parte da \(x_{0} = 0\) con \(v_{0} = 1,5\,\mathrm{m\,s^{-1}}\) e \(a = 0,60\,\mathrm{m\,s^{-2}}\). Dopo \(t = 4,0\,\mathrm{s}\): \(v = 1,5 + 0,60\cdot 4,0 = 3,9\,\mathrm{m\,s^{-1}}\); \(x = 0 + 1,5\cdot 4,0 + \tfrac{1}{2}\cdot 0,60\cdot 4,0^{2} = 6,0 + 4,8 = 10,8\,\mathrm{m}\).

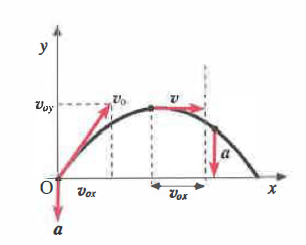
Moto parabolico con accelerazione costante. Si consideri ora un’accelerazione costante \(\mathbf{a}\) e una velocità iniziale \(\mathbf{v}_{0}\) non parallela ad \(\mathbf{a}\). La traiettoria non è più rettilinea. È conveniente introdurre un sistema cartesiano ortogonale \((x,y)\) con un asse parallelo ad \(\mathbf{a}\). Il moto si decompone in due moti monodimensionali accoppiati solo dal tempo. Assumendo \(\mathbf{a}\) lungo l’asse \(y\) e di verso opposto a quello positivo si ottiene:

\[
x = x_{0} + v_{0x} t
\]

\[
y = y_{0} + v_{0y} t - \frac{a}{2} t^{2}
\]

Lungo \(y\) il moto è uniformemente accelerato con velocità iniziale \(v_{0y}\); lungo \(x\) l’accelerazione è nulla e il moto è uniforme. Eliminando il tempo dalle equazioni parametriche si ottiene l’equazione della traiettoria. Risolvendo la prima in \(t\) e sostituendo nella seconda, con \(x_{0} = 0\), \(y_{0} = 0\), segue:

\[
y = \frac{v_{0y}}{v_{0x}} x - \frac{a}{2 v_{0x}^{2}} x^{2}
\]

La formua (\[y = \frac{v_{0y}}{v_{0x}} x - \frac{a}{2 v_{0x}^{2}} x^{2}\]) descrive una parabola concava verso il basso (Figura 02.02-06). Il dominio fisico è limitato agli intervalli temporali in cui il punto è definito (ad esempio, per un proiettile, fino al contatto col suolo).

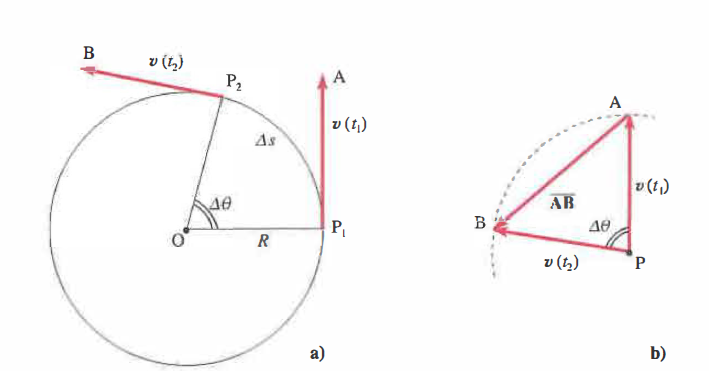
Moto circolare uniforme. Un punto \(P\) percorre una circonferenza di raggio \(R\) con velocità di modulo costante, mentre direzione e verso mutano continuamente (Figura 02.02-07). La velocità tangenziale o periferica è \(v\); la velocità angolare è \(\omega\), definita come rapporto tra l’angolo \(\Delta\theta\) spazzato dal raggio \(OP\) e l’intervallo di tempo \(\Delta t\):

\[
\omega = \frac{\Delta \theta}{\Delta t}
\]

Poiché \(\Delta s = \Delta\theta \cdot R\) (con \(\Delta\theta\) in radianti) e \(v = \Delta s / \Delta t\), segue la relazione fondamentale fra velocità periferica e angolare:

\[
v = \omega R
\]

Per l’accelerazione, si considerino i vettori velocità \( \mathbf{v}(t_{1})\) e \(\mathbf{v}(t_{2})\), uguali in modulo ma con direzioni diverse (Figura 02.02-07). Traslandoli con le origini coincidenti (Figura 02.02-07), la differenza \(\mathbf{v}(t_{2}) - \mathbf{v}(t_{1})\) sottende un angolo \(\Delta\theta = \omega \Delta t\). Per \(\Delta t\) piccolo, l’arco è ben approssimato dalla corda e si ha:

\[
|\mathbf{v}(t_{2}) - \mathbf{v}(t_{1})| \approx v \Delta \theta = v \omega \Delta t
\]

Ne consegue che il modulo dell’accelerazione risulta:

\[ a = \frac{\left|v(t_2) - v(t_1)\right|}{\Delta t} = v \omega = \frac{v^2}{R} = \omega^2 R \]

Quando \(\Delta t \to 0\), \(\mathbf{v}(t_{2})\) e \(\mathbf{v}(t_{1})\) coincidono, e la variazione di velocità risulta perpendicolare alla tangente: l’accelerazione è puramente normale, diretta verso il centro (centripeta), con componente tangenziale nulla. Dalle relazioni precedenti si ricavano anche periodo e frequenza: \(T = 2\pi/\omega\), \(\nu = 1/T\), \(v = 2\pi R / T\).

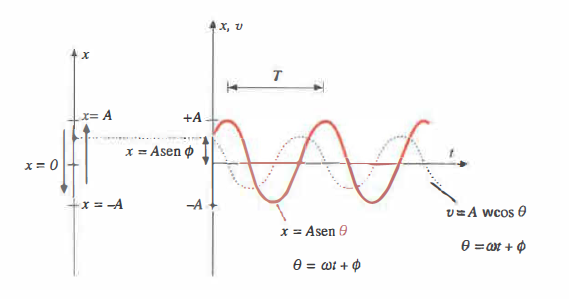
Moto armonico. Un punto materiale compie un moto periodico lungo un segmento, descritto da una legge sinusoidale:

\[ x = A \sin(\omega t + \phi) \]

Qui \(x\) è lo spostamento rispetto all’origine posta al centro dell’oscillazione; \(A\) è l’ampiezza; \(\omega\) è la pulsazione, legata alla frequenza \(\nu\) da \(\omega = 2\pi \nu\) e al periodo da \(\nu = 1/T\). L’angolo \(\phi\) è la fase iniziale: per \(t = 0\), \(x = A \sin \phi\), che individua la posizione iniziale (Figura 02.02-08). Ad ogni incremento di fase di \(2\pi\) lo spostamento si ripete, per cui \(T = 2\pi/\omega = 1/\nu\).

Derivando la legge oraria si ottengono velocità e accelerazione:

\[ v = +A \omega \cos(\omega t + \phi) \]

\[ a = -A\omega^2 \text{sen}(\omega t + \phi) \]

Poiché \(x = A \sin(\omega t + \phi)\), si ottiene la forma compatta:

\[ a = -\omega^{2} x \]

La \[ a = -\omega^{2} x \] mostra che l’accelerazione è proporzionale e opposta allo spostamento; il coefficiente di proporzionalità è \(\omega^{2}\). elazione di questo tipo caratterizza ogni moto armonico descritto dalla Formula (\[x = A \sin(\omega t + \phi)\])

Moti in tre dimensioni. Se \(\mathbf{v}_{0}\) e/o \(\mathbf{a}\) possiedono componenti non nulle lungo tutti e tre gli assi \(x, y, z\), il moto si sviluppa nello spazio tridimensionale (Figura 02.02-09). La legge vettoriale, valida per accelerazione costante, è

\[ \mathbf{r}(t) = \mathbf{r}_{0} + \mathbf{v}_{0} t + \tfrac{1}{2}\,\mathbf{a}\, t^{2}, \]

ossia, in componenti,

\[ x(t) = x_{0} + v_{0x} t + \tfrac{1}{2} a_{x} t^{2}, \quad y(t) = y_{0} + v_{0y} t + \tfrac{1}{2} a_{y} t^{2}, \quad z(t) = z_{0} + v_{0z} t + \tfrac{1}{2} a_{z} t^{2}. \]

Quando \(\mathbf{a}\) non è parallela a \(\mathbf{v}_{0}\), la traiettoria non è una retta e, in generale, non è piana:

• Per moti a velocità costante: grafico \(x\)-\(t\) lineare, pendenza \(v_{0}\);
• Per accelerazione costante lungo una direzione: \(v(t)\) lineare in \(t\), \(x(t)\) parabolica;
• Per composizione in più dimensioni con accelerazioni costanti: ogni componente segue le leggi monodimensionali, il tempo funge da parametro comune;
• Nel moto circolare uniforme: \(v = \omega R\), \(a_{c} = v^{2}/R = \omega^{2}R\), direzione radiale verso il centro;
• Nel moto armonico: \(x=A\sin(\omega t+\phi)\), \(v=A\omega\cos(\omega t+\phi)\), \(a=-\omega^{2}x\), con \(T=2\pi/\omega\).

Image Gallery

Moto rettilineo uniforme

Traiettoria (sopra), legge oraria e grafico spazio-tempo di un moto rettilineo uniforme.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Moto uniformemente accelerato

Traiettoria (sopra), grafico spazio-tempo e grafico velocità -tempo di un moto uniformemente accelerato.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Moto parabolico

Traiettoria parabolica che si ottiene quando un oggetto è sottoposto a un'accelerazione a costante e a una velocità iniziale v0 che non è parallela ad a. Si noti che la componente della velocità v0x​, perpendicolare ad a, rimane costante durante il moto.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Moto circolare uniforme

Moto circolare uniforme. (a) La velocità è tangente e costante in modulo. L'accelerazione ottenuta con la costruzione geometrica indicata in (b) risulta diretta come il raggio dell'orbita e verso il centro (accelerazione centripeta).

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Moto circolare uniforme

Moto circolare uniforme. (a) La velocità è tangente e costante in modulo. L'accelerazione ottenuta con la costruzione geometrica indicata in (b) risulta diretta come il raggio dell'orbita e verso il centro (accelerazione centripeta).

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Moto circolare uniforme

Moto circolare uniforme. (a) La velocità è tangente e costante in modulo. L'accelerazione ottenuta con la costruzione geometrica indicata in (b) risulta diretta come il raggio dell'orbita e verso il centro (accelerazione centripeta).

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Moto armonico – Diagrammi spazio-tempo e velocità -tempo

Diagramma spazio-tempo (linea rossa continua) e diagramma velocità -tempo (linea punteggiata) per un moto armonico.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.

Image Gallery

Moto a spirale tridimensionale

Una pallina si muove su una superficie a forma di imbuto. Se la velocità iniziale e/o l'accelerazione non sono dirette verso il centro dell'imbuto, ma obliquamente, e quindi possiedono tre componenti non nulle, il moto è una spirale in tre dimensioni.

Immagine tratta liberamente da Internet. Se viola i tuoi diritti, contattaci.