Lenti sottili
Definizione
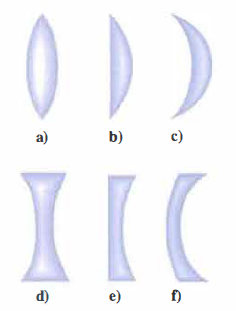
Le lenti sottili rappresentano un caso particolare dello studio dei sistemi diottrici centrati. Una lente sferica può essere trattata, nel limite paraassiale, come la successione di due superfici di separazione tra mezzi (diottri) con centri di curvatura allineati sull’asse ottico. Si dice “sottile” una lente il cui spessore assiale è trascurabile rispetto ai raggi di curvatura delle sue superfici e rispetto al diametro delle calotte che la costituiscono; in tale approssimazione i piani principali coincidono con il piano mediano della lente e si identifica un unico centro ottico: ogni raggio che attraversa il centro ottico non devia. Se la lente è in aria, è equivalente a un diottro aria–vetro seguito da un diottro vetro–aria. In (Figura 07.39-01) sono raggruppate le tipologie più comuni di lenti sottili.
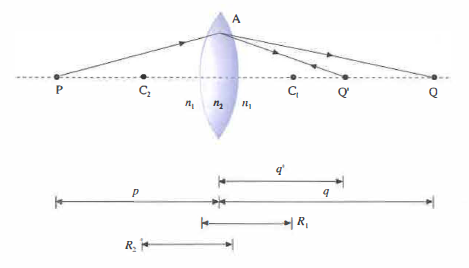
Come per il singolo diottro, anche per le lenti è essenziale la relazione dei punti coniugati, che qui si ricava applicando in sequenza la formula del diottro alle due superfici, rispettando la convenzione dei segni. Consideriamo una lente biconvessa di indice n₂, immersa in un mezzo omogeneo di indice n₁ (Figura 07.39-02). Indichiamo con R₁ e R₂ i raggi di curvatura delle due calotte: per convenzione, R > 0 se la superficie è convessa verso destra, R < 0 altrimenti. Per il primo diottro (aria–vetro) si ottiene
\[\displaystyle \frac{n_1}{p} + \frac{n_2}{q'} = \frac{n_2 - n_1}{R_1}.\]
L’immagine intermedia a distanza \(q'\) dal vertice della prima superficie funge da oggetto per il secondo diottro (vetro–aria), collocandosi nello spazio immagine di quest’ultimo. Si ha quindi
\[\displaystyle \frac{n_2}{q'} + \frac{n_1}{q} = \frac{n_1 - n_2}{R_2},\]
con \(R_2\) negativo nel caso illustrato, coerentemente con la convenzione. Sommando membro a membro si ottiene:
\[\displaystyle \frac{n_1}{p} + \frac{n_1}{q} = (n_2 - n_1) \!\left( \frac{1}{R_1} - \frac{1}{R_2} \right),\]
che, introducendo il rapporto degli indici \(n = n_2/n_1\), si scrive come relazione dei punti coniugati per una lente sottile:
\[\displaystyle \frac{1}{p} + \frac{1}{q} = (n - 1) \!\left( \frac{1}{R_1} - \frac{1}{R_2} \right).\]
Il centro ottico coincide con il centro geometrico della lente; in regime paraassiale le distanze focali oggettiva e immagine hanno lo stesso valore assoluto. Infatti, facendo tendere \(p \to \infty\) (quindi \(1/p \to 0\)) o, simmetricamente, \(q \to \infty\) nella (\frac{1}{p} + \frac{1}{q} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right).), si ricava un’unica espressione per la distanza focale \(f\):
\[\displaystyle \frac{1}{f} = (n - 1) \!\left( \frac{1}{R_1} - \frac{1}{R_2} \right).\]
Sostituendo la (\frac{1}{f} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right).) nella (\frac{1}{p} + \frac{1}{q} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right).) si ottiene la forma sintetica della relazione dei punti coniugati:
\[\displaystyle \frac{1}{p} + \frac{1}{q} = \frac{1}{f}.\]
Le equazioni precedenti sono valide nel quadro delle approssimazioni di Gauss: raggi vicini all’asse ottico e piccole aperture, così da trascurare le aberrazioni (sferica, coma, astigmatismo, curvatura di campo e distorsione). Dalle (\frac{1}{f} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right).) e (\frac{1}{p} + \frac{1}{q} = \frac{1}{f}.) si evince che l’azione della lente dipende sia dalla forma (segni e moduli di \(R_1\) e \(R_2\)) sia dal rapporto fra indici \(n = n_2/n_1\). Una lente biconvessa, convergente in aria, può diventare divergente se immersa in un mezzo con indice più alto del vetro: se \(n_1 > n_2\), allora \(n - 1 < 0\) e \(f\) cambia segno.
Per convenzione, si distinguono:
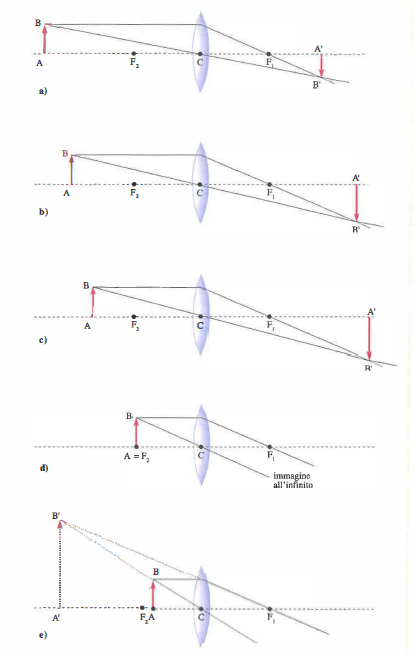
- lenti convergenti, con \(f > 0\), che raccolgono un fascio parallelo in un fuoco reale F (Figura 07.39-03);
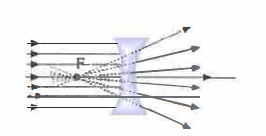
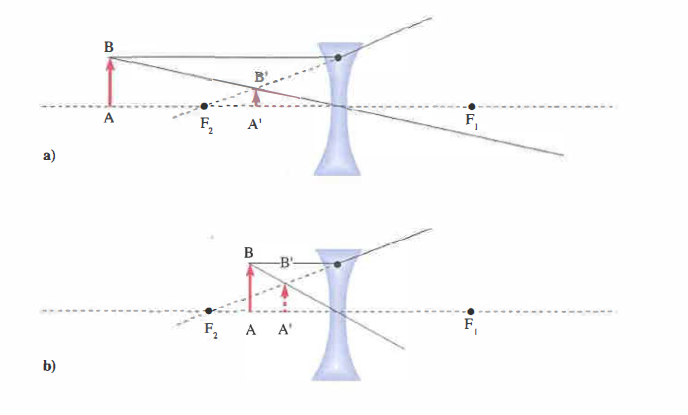
- lenti divergenti, con \(f < 0\), che fanno divergere il fascio come se provenisse da un fuoco virtuale F (Figura 07.39-04).
Le caratteristiche qualitative dei principali profili di lente sono riepilogate in (Tabella 07.39-01). Si definisce potere diottrico \(\Psi\) l’inverso della distanza focale espressa in metri:
\[\displaystyle \Psi = \frac{1}{f}.\]
Il potere si misura in diottrie (m⁻¹). Esempi: una lente di +4,0 D ha \(f = 0,25\) m (convergente), mentre una lente di −3,0 D ha \(f = -0,333\) m (divergente). Il segno di \(\Psi\) coincide con quello di \(f\).
| Tipo di lente | Raggi di curvatura (R₁, R₂) | Fuoco (f) | Comportamento ottico |
|---|---|---|---|
| Biconvessa | R₁ > 0 ; R₂ < 0 | f > 0 | Convergente |
| Piano-convessa | R₁⁻¹ = 0 ; R₂ < 0 oppure R₁ > 0 ; R₂⁻¹ = 0 | f > 0 | Convergente |
| Concavo-convessa | R₁ > R₂ (maggiore curvatura esterna) | f > 0 | Convergente |
| Biconcava | R₁ < 0 ; R₂ > 0 | f < 0 | Divergente |
| Piano-concava | R₁⁻¹ = 0 ; R₂ > 0 oppure R₁ < 0 ; R₂⁻¹ = 0 | f < 0 | Divergente |
| Concavo-convessa | R₁ < R₂ (maggiore curvatura interna) | f < 0 | Divergente |
| Lente cilindrica | Curvatura su un solo asse | variabile | Correzione astigmatismo |
| Lente prismatica | Non ha fuoco proprio | deviazione | Usata in diplopia/strabismo |
| Lente menisco positiva | Superficie convessa > concava | f > 0 | Convergente (occhiali ipermetropia) |
| Lente menisco negativa | Superficie concava > convessa | f < 0 | Divergente (occhiali miopia) |
Caratteristiche di lenti sottili con indice n > 1
Proprietà ottiche dei diversi tipi di lenti sottili.
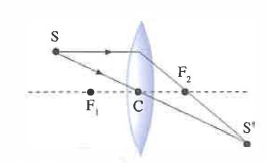
Un punto oggetto decentrato rispetto all’asse, purché sufficientemente vicino ad esso e con raggi incidenti di piccola apertura, genera un punto immagine ben definito, come in (Figura 07.39-05). Per la costruzione grafica bastano due raggi principali:
- il raggio parallelo all’asse, che dopo la rifrazione passa per il fuoco immagine F per lenti convergenti, oppure sembra provenire da F per lenti divergenti;
- il raggio passante per il centro ottico, che attraversa la lente senza deviazione.
L’intersezione dei due raggi rifratti determina il punto immagine S′ di S. Un oggetto esteso si considera come un insieme di punti; l’immagine complessiva si ottiene componendo le immagini dei singoli punti. La posizione dell’immagine varia con la collocazione dell’oggetto: esempi per una biconvessa sono in (Figura 07.39-06) e per una biconcava in (Figura 07.39-07).
L’ingrandimento lineare \(G\) è il rapporto tra la dimensione trasversa dell’immagine \(\overline{\text{A}'\text{B}'}\) e quella dell’oggetto \(\overline{\text{AB}}\). Dalla similitudine dei triangoli, insieme alla (\frac{1}{p} + \frac{1}{q} = \frac{1}{f}.), si ottiene
\[\displaystyle G = \frac{\overline{\text{A}'\text{B}'}}{\overline{\text{AB}}} = \frac{|q|}{|p|} = \frac{|f|}{|p - f|} = \left| \frac{q - f}{f} \right|.\]
Nel formalismo con segni, \(G = -\,q/p\): il segno negativo indica inversione dell’immagine rispetto all’oggetto quando l’immagine è reale. Come esempio distinto dai precedenti, una lente con \(f = +10,0\) cm e un oggetto a \(p = 15,0\) cm dà \(q = \frac{fp}{p - f} = 30,0\) cm e \(G = -\,q/p = -2,0\), immagine reale e capovolta di doppie dimensioni.
Per due lenti sottili a contatto, di focali \(f_1\) e \(f_2\), il sistema è equivalente a una singola lente di focale
\[\displaystyle \frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2}.\]
In termini di potere, \(\Psi = \Psi_1 + \Psi_2\) per lenti a contatto. Se le lenti sono separate da una distanza \(d\), l’equivalente focale in aria si modifica secondo \(\displaystyle \frac{1}{f_{\text{eq}}} = \frac{1}{f_1} + \frac{1}{f_2} - \frac{d}{f_1 f_2}\), con i fuochi non più simmetrici rispetto alle singole lenti. L’ingrandimento totale di un sistema di lenti sottili in cascata è il prodotto degli ingrandimenti delle singole lenti: \(G = G_1 G_2\), assumendo che l’uscita di una lente fornisca l’oggetto (reale o virtuale) per la successiva.