Quantità sperimentali
Definizione
Le misure sperimentali forniscono il linguaggio quantitativo della scienza: dati espressi con unità appropriate e un numero coerente di cifre significative. Tra le grandezze di uso più frequente spiccano massa, lunghezza, volume, tempo, temperatura ed energia. La scelta dell’unità deve essere commisurata all’ordine di grandezza del fenomeno osservato, così da ottenere valori numericamente prossimi a \(10^{0}\) ed evitare esponenti estremi, facilitando confronto e calcolo.
La massa quantifica la quantità di materia in un sistema ed è una proprietà intrinseca, indipendente dal luogo in cui si trova l’oggetto. Il termine peso, spesso usato colloquialmente come sinonimo, indica invece una forza dovuta al campo gravitazionale locale e si esprime come:
\(P = m\,g\)
dove \(m\) è la massa e \(g\) l’accelerazione di gravità, che sulla superficie terrestre è circa \(9,81\,\mathrm{m\,s^{-2}}\) ma non è costante, variando con latitudine, altitudine e geologia. Proprio perché \(g\) cambia, il peso non è un indicatore affidabile della quantità di materia. La massa, al contrario, si determina per confronto con campioni di riferimento mediante bilance. La (Figura 01.05-01) illustra alcuni modelli di bilance utilizzati comunemente per misure in laboratorio.
Nella misura di enti microscopici, come atomi e molecole, unità macroscopiche come grammo (g) o microgrammo (µg) risultano inadatte. Si usa allora l’unità di massa atomica unificata, definita come \(1/12\) della massa dell’atomo di carbonio-12: \(1\,\text{u} \approx 1,6605 \times 10^{-24}\,\text{g}\). Per confronto, la massa di un atomo di idrogeno è circa \(1,6735 \times 10^{-24}\,\text{g}\), mentre quella di un atomo di ossigeno è circa \(2,656 \times 10^{-23}\,\text{g}\). Nella pratica sperimentale è opportuno selezionare l’unità in modo che i valori numerici ottenuti siano compatti e di lettura immediata.
La lunghezza, intesa come distanza tra due punti, nel Sistema Internazionale (SI) ha come unità base il metro (m). Per intervalli estesi si usano i chilometri (km), mentre a scale più ridotte si impiegano centimetri (cm) e millimetri (mm). Le distanze molecolari e interatomiche ricadono tipicamente nel dominio dei nanometri (nm) o degli angström (Å):
\(1\,\mathrm{nm} = 10^{-9}\,\mathrm{m} = 10^{-7}\,\mathrm{cm}\)
\(1\,\mathrm{Å} = 10^{-10}\,\mathrm{m} = 10^{-8}\,\mathrm{cm}\)
In fisica atomica si adottano talvolta i picometri (pm), con \(1\,\mathrm{pm} = 10^{-12}\,\mathrm{m}\), adatti a descrivere raggi atomici e lunghezze di legame.
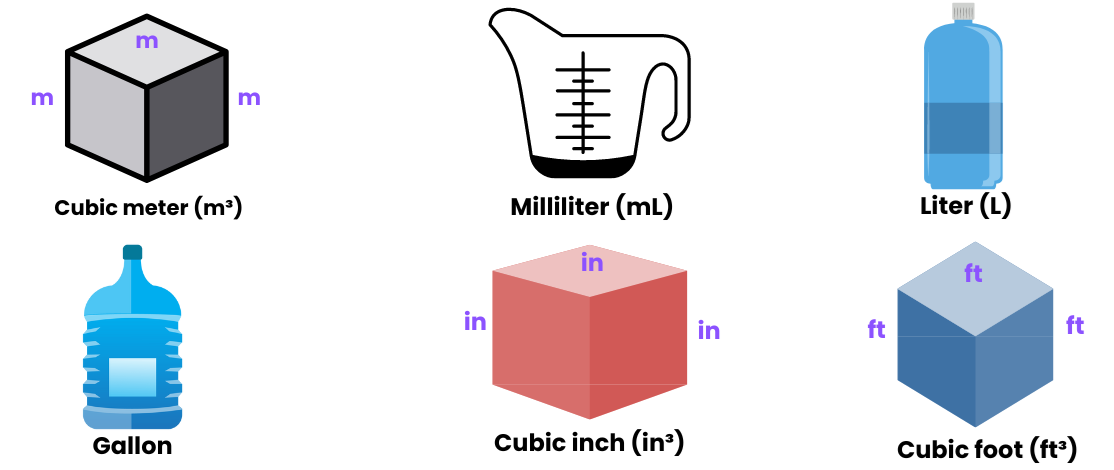
Il volume esprime lo spazio occupato da un corpo. Nel SI l’unità derivata è il metro cubo (\(\mathrm{m^{3}}\)), ma in chimica è d’uso il litro (L), con \(1\,\mathrm{L} = 1\,\mathrm{dm^{3}} = 10^{-3}\,\mathrm{m^{3}}\). La relazione tra L e mL è schematizzata in (Figura 01.05-02). In laboratorio si impiegano strumenti di misura tarati in millilitri (mL) o microlitri (µL), come mostrato in (Figura 01.05-03), con la corrispondenza fondamentale \(1\,\mathrm{mL} = 1\,\mathrm{cm^{3}}\).
Gli strumenti volumetrici si distinguono in “to contain” (TC) e “to deliver” (TD): i matracci tarati contengono un volume esatto alla temperatura di taratura, mentre cilindri graduati, pipette e burette sono progettati per erogare volumi noti con precisione. La scelta dello strumento dipende dall’incertezza richiesta e dal volume da misurare.
Il tempo ha come unità il secondo (s). La sua misura è cruciale quando l’evoluzione di un sistema dipende dalla dinamica, per esempio nelle cinetiche di reazione o nei processi di diffusione. La velocità di reazione è una funzione della variazione della concentrazione nel tempo; la caratterizzazione temporale consente di dedurre meccanismi, ordini di reazione e costanti cinetiche.
La temperatura quantifica lo stato termico di un sistema e, a livello microscopico, è correlata all’energia cinetica media delle particelle. È distinta dal calore, che è energia in transito tra sistemi a causa di una differenza di temperatura. Un medesimo incremento di calore può produrre variazioni di temperatura diverse a seconda della massa e della capacità termica del materiale.
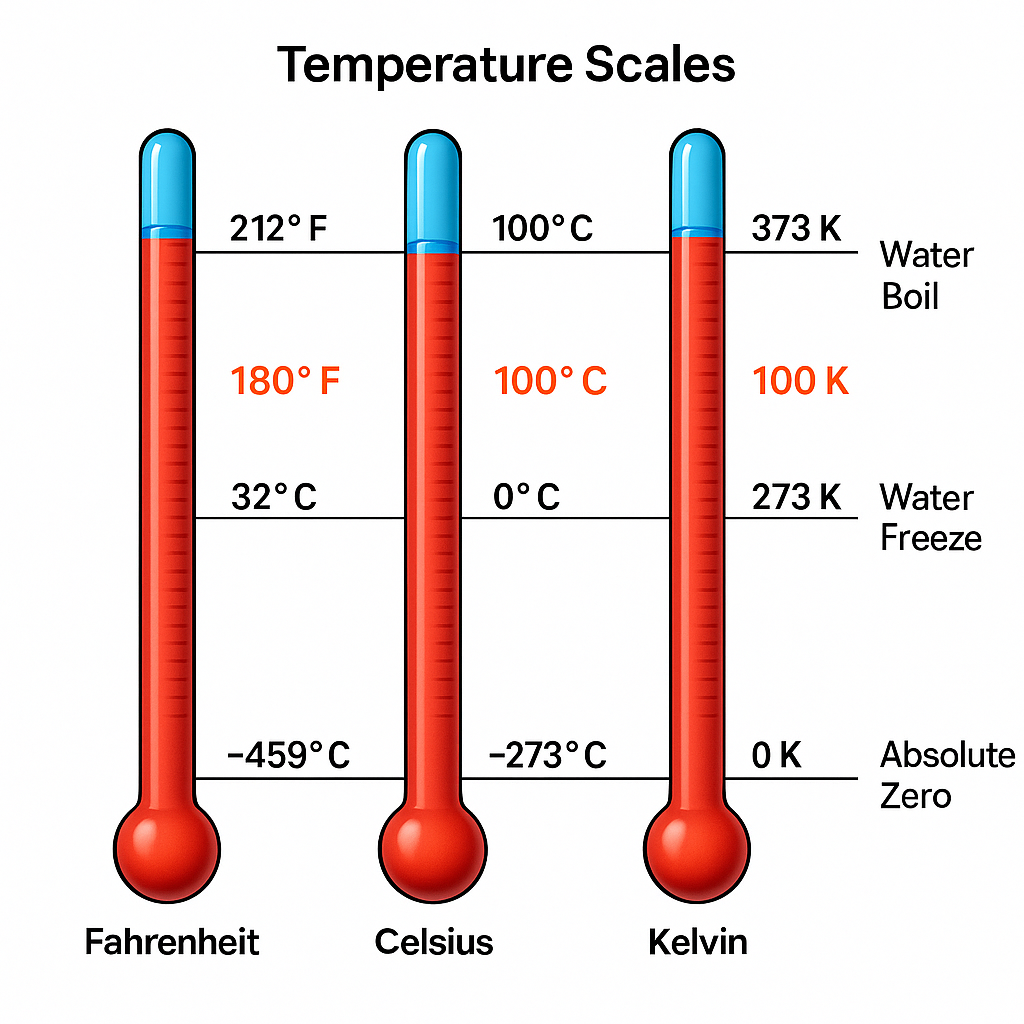
Molti materiali si espandono al crescere di temperatura; tale proprietà consente la costruzione di termometri, ad esempio a mercurio o ad alcol, in cui l’altezza della colonna è proporzionale alla temperatura. Le scale di uso più comune in ambito scientifico sono Celsius (°C) e Kelvin (K). Il Kelvin è la scala termodinamica assoluta, con zero corrispondente allo zero assoluto. Le temperature di riferimento per la taratura includono la solidificazione e l’ebollizione dell’acqua. La (Figura 01.05-04) riporta i punti di riferimento e le corrispondenze tra le scale. La conversione tra Celsius e Kelvin è data da:
\(T_{\mathrm{K}} = t_{\mathrm{°C}} + 273,15\)
In contesti tecnici può comparire la scala Fahrenheit (°F), sebbene non sia standard nel SI.
L’energia è la capacità di compiere lavoro o di trasferire calore. Si classificano comunemente energia cinetica (associata al moto) ed energia potenziale (associata alla posizione o alla configurazione). Per forma fisica si distinguono, tra le altre, energia luminosa, termica, elettrica, meccanica e chimica. Alcune proprietà generali sono fondamentali:
- in un sistema isolato l’energia totale si conserva, non viene creata né distrutta;
- l’energia può trasformarsi da una forma a un’altra, ad esempio da chimica a termica o meccanica;
- ogni conversione reale è caratterizzata da efficienza inferiore al 100%, con una parte dell’energia che degrada a calore disperso;
- le reazioni chimiche comportano sempre variazioni energetiche, con scambio di calore con l’ambiente a seconda che siano eso- o endotermiche.
Nel SI l’unità dell’energia è il joule (J), con \(1\,\mathrm{J} = 1\,\mathrm{kg\,m^{2}\,s^{-2}}\). In calorimetria è tradizionale la caloria (cal), legata al joule dalla relazione:
\(1\,\mathrm{cal} = 4,184\,\mathrm{J}\)
Una caloria è la quantità di calore necessaria per innalzare di \(1\,^{\circ}\mathrm{C}\) la temperatura di \(1\,\mathrm{g}\) d’acqua (in condizioni specificate). La quantità di calore scambiata da una sostanza al variare della temperatura si calcola con \(q = m\,c\,\Delta T\), dove \(c\) è il calore specifico. La temperatura è una proprietà intensiva, mentre l’entalpia (contenuto di calore a pressione costante) è estensiva, poiché dipende dalla quantità di sostanza. Non tutti i materiali immagazzinano calore nello stesso modo: per innalzare di \(1\,^{\circ}\mathrm{C}\) la temperatura di \(1\,\mathrm{g}\) di ferro occorrono circa \(0,108\,\mathrm{cal}\), mentre per \(1\,\mathrm{g}\) d’acqua servono \(1,00\,\mathrm{cal}\) (equivalenti a circa \(0,452\,\mathrm{J\,g^{-1}\,K^{-1}}\) e \(4,18\,\mathrm{J\,g^{-1}\,K^{-1}}\), rispettivamente).
Massa e volume sono proprietà estensive; dal loro rapporto si ottiene la densità, grandezza intensiva che non dipende dalla quantità di sostanza. Per definizione:
\(\rho = \dfrac{m}{V}\)

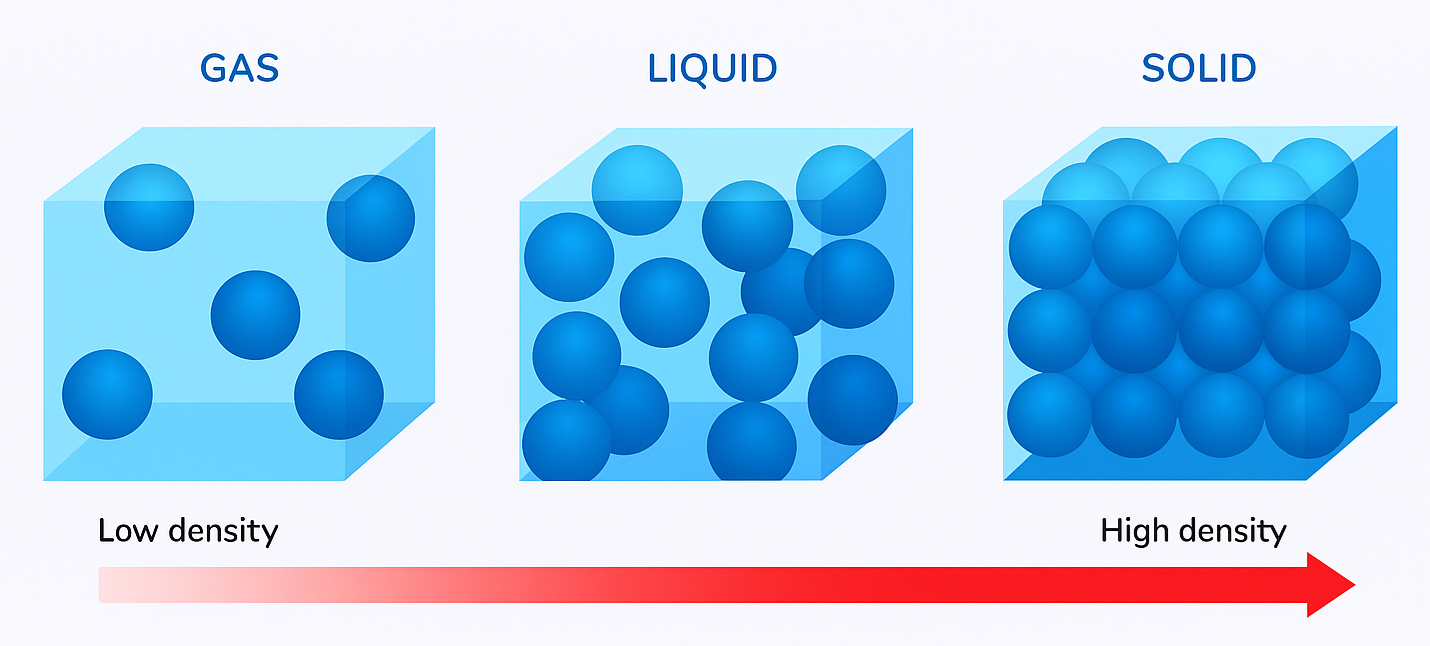
La densità costituisce un parametro utile per caratterizzare o identificare sostanze pure, poiché a una data temperatura e pressione ciascuna sostanza presenta un valore tipico (Figura 01.05-05). In chimica si esprime comunemente in \(\mathrm{g\,mL^{-1}}\), \(\mathrm{g\,cm^{-3}}\) o \(\mathrm{g\,cc^{-1}}\), ricordando che \(1\,\mathrm{mL} = 1\,\mathrm{cm^{3}} = 1\,\mathrm{cc}\). La densità dipende dalla temperatura (e, per i gas, anche dalla pressione), aspetto da controllare nelle misure e nei confronti tabulati.
Campioni di ugual volume di sostanze diverse hanno masse differenti: \(1\,\mathrm{mL}\) di ferro risulta molto più pesante di \(1\,\mathrm{mL}\) d’aria, coerentemente con le rispettive densità. Storicamente, la determinazione della densità ha permesso di distinguere l’oro autentico da leghe meno dense; ancora oggi è una tecnica analitica di base. La gravità specifica (o densità relativa) è il rapporto tra la densità della sostanza e quella dell’acqua a \(4\,^{\circ}\mathrm{C}\); è adimensionale e facilita confronti immediati. Metodi di misura includono picnometri, densimetri e bilance idrostatiche. La densità di alcune sostanze comuni è riportata nella (Tabella 01.05-01).
| Sostanza | Densità (g/mL) | Sostanza | Densità (g/mL) |
|---|---|---|---|
| Aria | 0.00129 (a 0 °C) | Alcol metilico | 0.792 |
| Ammoniaca | 0.000771 (a 0 °C) | Latte | 1.028–1.035 |
| Benzene | 0.879 | Ossigeno | 0.00143 (a 0 °C) |
| Osso | 1.7–2.0 | Gomma | 0.9–1.1 |
| Anidride carbonica | 0.001963 (a 0 °C) | Trementina | 0.87 |
| Alcol etilico | 0.789 | Urina | 1.010–1.030 |
| Gasolio | 0.66–0.69 | Acqua (4 °C) | 1.000 |
| Oro | 19.3 | Acqua (20 °C) | 0.998 |
| Idrogeno | 0.000090 (a 0 °C) | Legno (balsa, il legno a minor densità; ebano e teak, tra i più elevati in densità) | 0.3–0.98 |
| Cherosene | 0.82 | ||
| Piombo | 11.3 | Mercurio | 13.6 |
| Sangue (extra) | ~1.060 | Plasma (extra) | ~1.025 |
| Glicerina (extra) | 1.26 | Olio d’oliva (extra) | ~0.92 |
Densità dei materiali più diffusi
Valori tipici di densità per materiali comunemente utilizzati.