Luce, struttura atomica e atomo di Bohr
Definizione
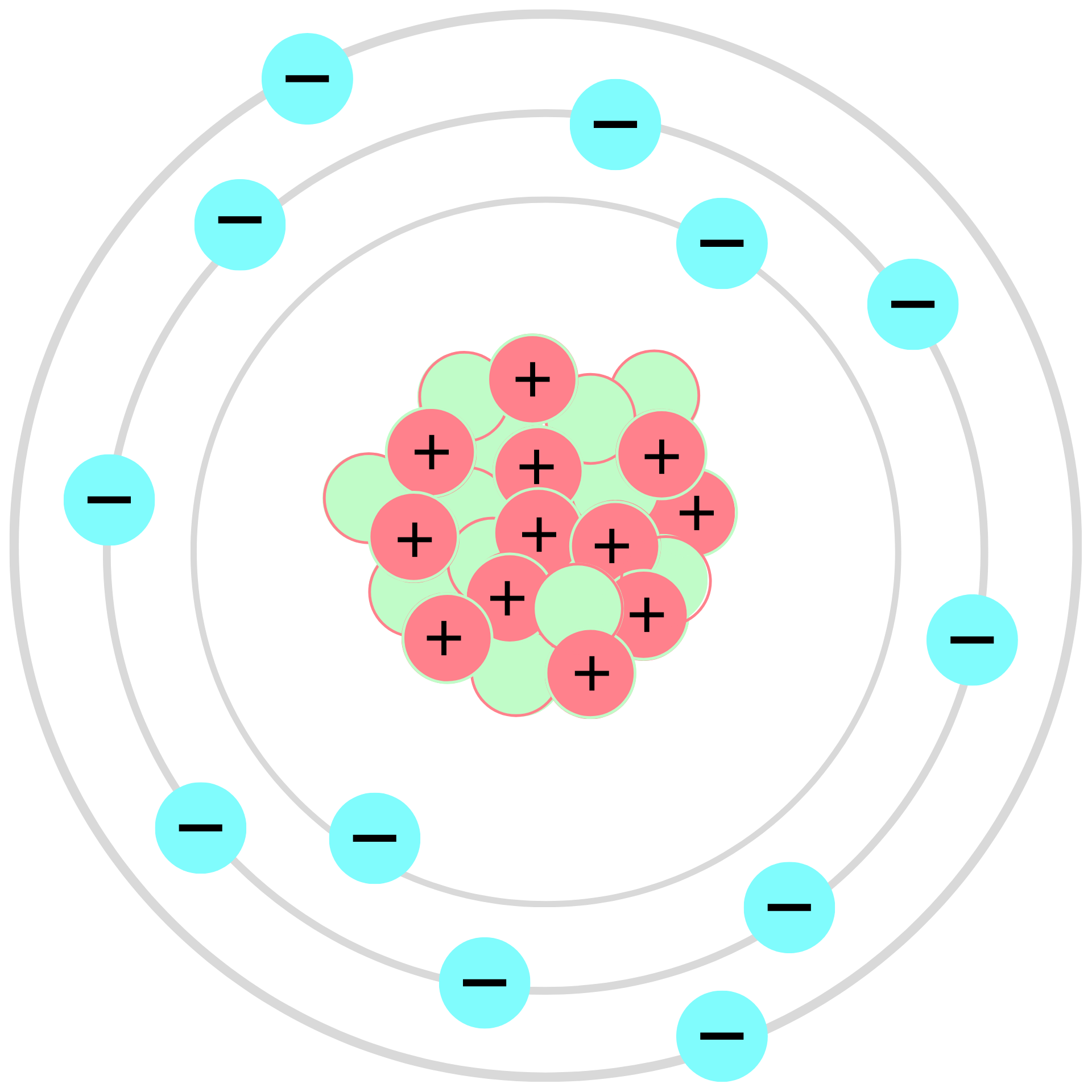
Il modello nucleare di Rutherford descrive l’atomo come un nucleo minuscolo, molto denso e positivamente carico, attorno al quale si trovano gli elettroni. Tale quadro, pur corretto a grandi linee, non specifica come gli elettroni siano organizzati né come interagiscano tra loro e con il nucleo. Alle scale dell’ordine di 10−9 m, gli strumenti classici per localizzare particelle perdono efficacia; risulta invece più produttivo misurare variazioni di energia, tramite fenomeni di assorbimento ed emissione di luce. L’insieme di tecniche che correlano la luce emessa o assorbita con la struttura interna della materia prende il nome di spettroscopia.
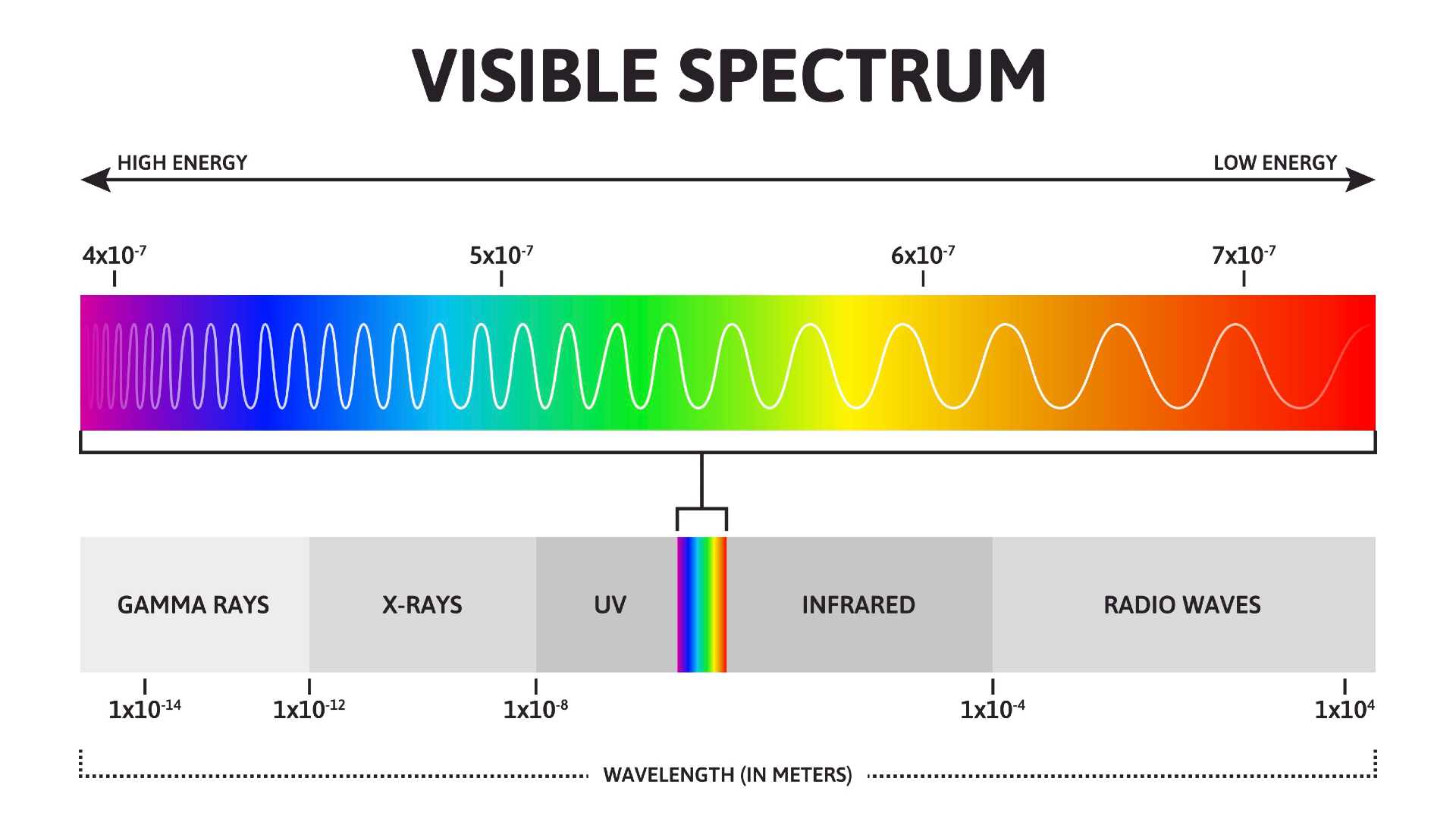
La luce è una forma di radiazione elettromagnetica che si propaga sotto forma di onde emesse da una sorgente, come il Sole. L’esperienza quotidiana dell’arcobaleno, oppure la scomposizione della luce bianca attraverso un prisma di vetro (Figura 01.08-01), mostra che la radiazione visibile è costituita da componenti di diverso colore, ciascuna caratterizzata da una distinta lunghezza d’onda. Una radiazione ondulatoria può essere rappresentata come un’onda sinusoidale; la lunghezza d’onda, indicata con \( \lambda \), è la distanza tra due massimi consecutivi.
 |
| Onda periodica – lunghezza d’onda e oscillazione nel tempo |
Tutte le radiazioni elettromagnetiche nel vuoto si muovono con la stessa velocità, la velocità della luce, pari a \( c \approx 3{,}00 \times 10^{8} \) m/s. A ogni lunghezza d’onda è associata una frequenza \( \nu \) e vale la relazione fondamentale
[ c = \lambda \, \nu. ]
L’energia della radiazione è quantizzata e si esprime in termini del quanto di luce, il fotone. Per un fotone vale
[ E = h \nu = \frac{h c}{\lambda}, ]
dove \( h \) è la costante di Planck. Ne segue che lunghezza d’onda ed energia sono inversamente correlate: onde più “corte” trasportano più energia. L’insieme di tutte le lunghezze d’onda costituisce lo spettro elettromagnetico, convenzionalmente suddiviso in regioni (Figura 01.08-02) con proprietà fisiche peculiari: raggi gamma e X (altissima energia), ultravioletto, visibile, infrarosso, microonde e onde radio. Per esempio, una microonda tipica di \( \lambda = 0{,}12 \) m ha \( \nu \approx 2{,}5 \) GHz, mentre una radiazione visibile blu di \( \lambda = 450 \) nm ha energia per fotone sensibilmente più elevata.
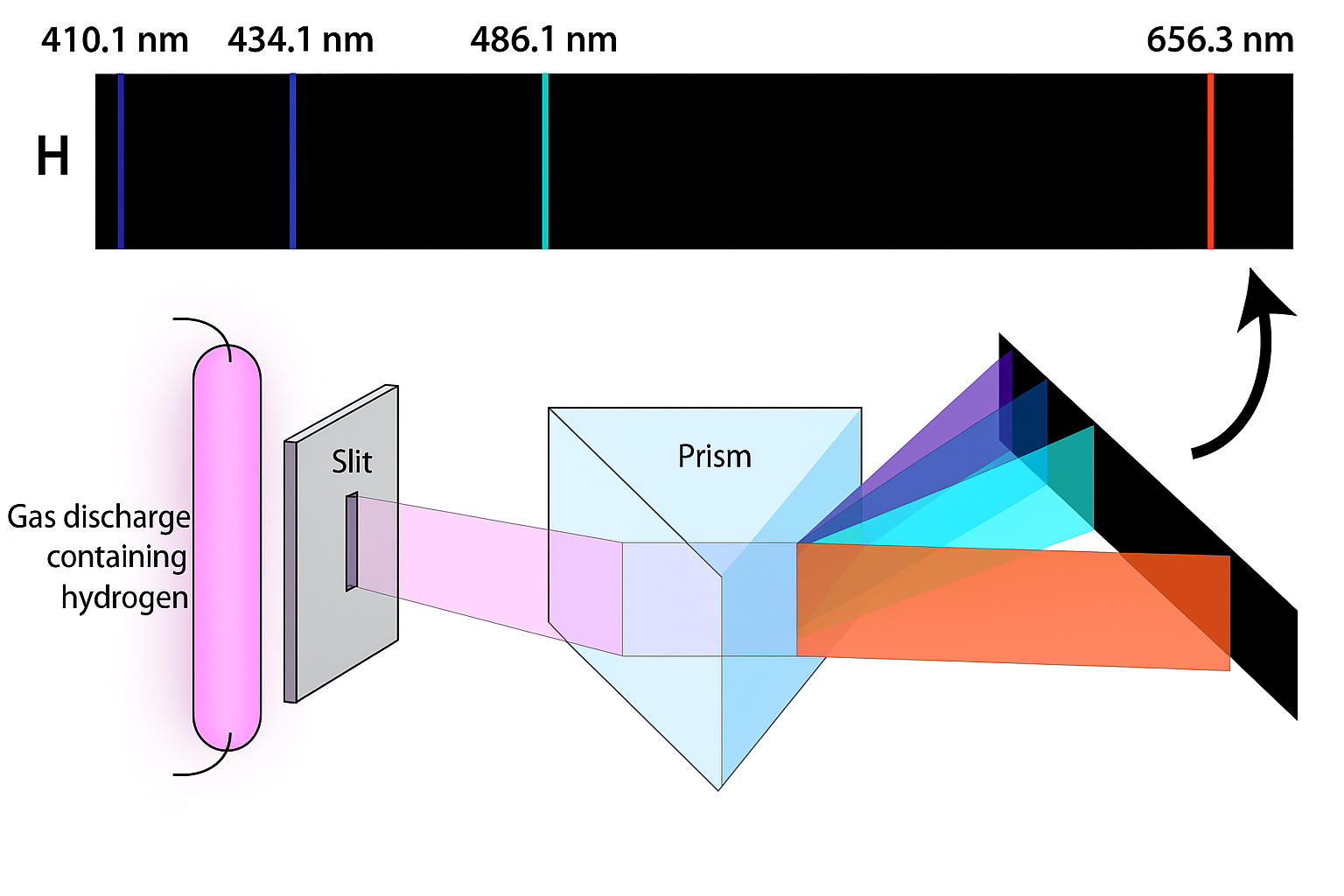
Informazioni decisive sulla struttura atomica emergono dagli spettri. Se un gas rarefatto, come l’idrogeno, è contenuto in un tubo evacuato con due elettrodi e viene percorso da una scarica, il gas emette luce. Analizzando tale luce, non si osserva un continuo di lunghezze d’onda, ma un insieme di righe ben definite: lo spettro a righe di emissione (Figura 01.08-03). Gas diversi (per esempio elio o neon) generano insiemi differenti di righe, fungendo da “impronte digitali” dell’elemento. La spiegazione di questo comportamento porta al modello di Bohr.
Niels Bohr propose che gli elettroni possano occupare solo certi livelli energetici ben determinati, associati a orbite circolari quantizzate attorno al nucleo. Questa ipotesi introdusse la quantizzazione dell’energia: transizioni tra livelli sono possibili solo assorbendo o emettendo quantità discrete di energia. Quando un elettrone assorbe energia, passa da un’orbita più interna (energia minore) a una più esterna (energia maggiore), generando uno stato eccitato; il processo inverso, con emissione di un fotone di energia pari alla differenza tra i due livelli, riporta il sistema verso stati a energia inferiore fino, eventualmente, allo stato fondamentale (Figura 01.08-04). La condizione di risonanza energetica è
[ \Delta E = E_{\text{alto}} - E_{\text{basso}} = h \nu = \frac{h c}{\lambda}. ]
Nel caso dell’idrogeno, il modello di Bohr fornisce espressioni quantitative per le energie dei livelli consentiti:
[ E_n = - \frac{R_H h c}{n^2} = - \frac{13{,}6 \ \text{eV}}{n^2}, \quad n = 1, 2, 3, \ldots ]
dove \( R_H \) è la costante di Rydberg per l’idrogeno. Le transizioni tra questi livelli generano serie di righe spettrali, descritte dalla formula di Rydberg:
[ \frac{1}{\lambda} = R_\infty \!\left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right), \quad n_2 > n_1, ]
con \( R_\infty \approx 1{,}097 \times 10^{7} \ \text{m}^{-1} \). Le righe visibili dell’idrogeno appartengono alla serie di Balmer (transizioni verso \( n_1 = 2 \)).
Esempio numerico didatticamente equivalente: per la transizione \( n_2 = 5 \to n_1 = 2 \), si ha
[ \frac{1}{\lambda} = R_\infty \!\left(\frac{1}{4} - \frac{1}{25}\right) = R_\infty \cdot \frac{21}{100} \approx 2{,}3037 \times 10^{6} \ \text{m}^{-1}, ]
da cui \( \lambda \approx 4{,}341 \times 10^{-7} \ \text{m} = 434{,}1 \ \text{nm} \) (violetto). L’energia del fotone è \( E = h c / \lambda \approx 2{,}86 \ \text{eV} \).
È utile associare a ciascun livello un numero quantico principale \( n \) (1, 2, 3, …), che cresce con la distanza media dal nucleo e con l’energia. Nel linguaggio del modello di Bohr, i livelli a energia maggiore corrispondono a orbite più ampie.
In sintesi, le implicazioni operative del modello possono essere elencate come segue:
- gli elettroni sono ammessi solo in insiemi discreti di energie, i livelli consentiti;
- il passaggio tra livelli avviene per assorbimento o emissione di fotoni con energia \( \Delta E = h \nu \);
- le righe spettrali corrispondono a differenze di energia tra coppie di livelli permessi ed hanno lunghezza d’onda determinabile;
- i livelli energetici dell’idrogeno sono dati da \( E_n = -13{,}6/n^2 \) e spiegano la posizione delle righe osservate;
- livelli più energetici sono, in media, associati a distanze maggiori dal nucleo;
- dalle lunghezze d’onda misurate si ricavano le differenze di energia tra stati, fornendo una mappa quantitativa della struttura dei livelli.
Il modello di Bohr stabilì un nesso decisivo tra struttura atomica e spettri, introducendo i livelli energetici principali e la quantizzazione delle transizioni. Tuttavia, la sua validità è essenzialmente limitata a sistemi “idrogenoidi” (un solo elettrone). L’affinamento sperimentale e teorico ha mostrato discrepanze anche per l’idrogeno quando si considerano effetti più sottili, e il vincolo di orbite circolari fisse è risultato eccessivo.
La meccanica quantistica a onde, sviluppata successivamente, supera tali limiti. In essa l’elettrone è descritto da una funzione d’onda \( \psi \), e la quantità osservabile è la densità di probabilità \( |\psi|^2 \), che indica dove è più probabile trovare l’elettrone. Le regioni di spazio in cui la probabilità è elevata sono gli orbitali atomici. Tali orbitali sono organizzati in livelli energetici principali (identificati da \( n \)) e in sottolivelli o sottostrutture (caratterizzati da ulteriori numeri quantici), con forme e orientazioni specifiche nello spazio. La “nuvola elettronica” non rappresenta un percorso orbitale, ma una distribuzione di carica, più densa nelle zone a maggiore probabilità.
Questa impostazione è coerente con il principio di indeterminazione di Heisenberg, secondo cui posizione e quantità di moto non possono essere determinate simultaneamente con precisione arbitraria. Ne deriva l’abbandono dell’idea di traiettorie classiche e l’adozione di un quadro probabilistico che, pur mantenendo la quantizzazione energetica, descrive con accuratezza gli atomi multielettronici e rende conto di proprietà chimiche e fisiche, dei legami e delle tendenze periodiche.
In conclusione, la nozione di livelli energetici introdotta da Bohr resta un pilastro per interpretare gli spettri (Figura 01.08-03) e (Figura 01.08-04), mentre il formalismo moderno degli orbitali atomici, con i relativi numeri quantici e le funzioni d’onda, fornisce la descrizione quantitativa oggi accettata della struttura elettronica degli atomi e delle loro trasformazioni.