Atomi e concetto di mole
Definizione
La stechiometria descrive i rapporti quantitativi tra sostanze che reagiscono e prodotti che si formano, traducendo i processi chimici in relazioni numeriche utili alla progettazione e al controllo dei processi. Si consideri, a titolo di esempio, un impianto che intenda sintetizzare 800 kg di un intermedio farmaceutico: quanta materia prima occorre acquistare? Quale budget destinare ai reagenti se il fornitore prezza i composti a 18 € per grammo? Tali domande trovano risposta se si dispone di una “ricetta” affidabile: un’equazione chimica correttamente bilanciata. I coefficienti stechiometrici, infatti, definiscono i rapporti molari tra reagenti e prodotti e, insieme al concetto di mole, consentono di passare da quantità di sostanza a masse e numeri di particelle con calcoli rigorosi.
Gli atomi sono entità estremamente minute, ma le loro masse sono state determinate sperimentalmente per tutti gli elementi. L’unità di riferimento è l’unità di massa atomica, indicata con u (o uma): 1 u ≈ 1,661 × 10⁻²⁴ g. Per costruzione, 1 u è pari a 1/12 della massa di un atomo di carbonio-12 allo stato fondamentale. Questo collegamento con il carbonio-12 rende confrontabili le masse degli atomi e spiega perché le masse riportate in tavola periodica siano medie ponderate che riflettono l’abbondanza naturale degli isotopi.
Storicamente, la mole è stata definita come la quantità di sostanza che contiene tante entità elementari (atomi, molecole, ioni, elettroni o altre particelle) quante ne sono presenti in 12 g di carbonio-12. Dal 2019, nel Sistema Internazionale la definizione è divenuta operativa in termini della costante di Avogadro: la mole è la quantità di sostanza contenente esattamente \(N_\mathrm{A} = 6{,}022\,140\,76 \times 10^{23}\ \mathrm{mol^{-1}}\) entità elementari. Le due formulazioni sono coerenti, ma la seconda fissa \(N_\mathrm{A}\) come valore esatto, migliorando la tracciabilità metrologica.
La pratica di contare per “pacchetti” è comune nella vita quotidiana (una dozzina, una risma). Analogamente, 1 mol corrisponde a \(6{,}022 \times 10^{23}\) unità di qualunque oggetto; in chimica, tipicamente si tratta di atomi, ioni o molecole. La relazione tra unità di massa atomica e mole è particolarmente utile: la massa atomica media di un elemento espressa in u coincide numericamente con la massa di 1 mol di suoi atomi espressa in grammi, cioè con la massa molare \(M\) in g/mol. In simboli:
\[ M\ (\mathrm{g\ mol^{-1}}) \equiv \text{massa atomica in u} \]
Per esempio, un atomo di idrogeno ha massa media 1,008 u, dunque 1 mol di atomi di H ha massa 1,008 g; un atomo di carbonio ha massa media 12,01 u, quindi 1 mol di C pesa 12,01 g. Il numero di particelle in 1 mol è identico per tutti gli elementi, ma le masse molari possono differire enormemente: 1 mol di H ha massa 1,008 g, mentre 1 mol di Pb pesa 207,19 g (Figura 04.01-01).
Alcune precisazioni utili dal punto di vista metrologico:
- unità di massa atomica: \(1\ \mathrm{u} = \frac{1}{12} m(^{12}\mathrm{C}) \approx 1{,}6605 \times 10^{-27}\ \mathrm{kg} = 1{,}661 \times 10^{-24}\ \mathrm{g}\);
- costante di Avogadro: \(N_\mathrm{A} = 6{,}022\,140\,76 \times 10^{23}\ \mathrm{mol^{-1}}\) (valore esatto);
- identità numerica: massa in u di un atomo = massa in g di 1 mol dello stesso atomo.
Per convertire tra numero di particelle, moli e massa occorrono fattori di conversione affidabili. Le relazioni fondamentali sono:
\[ \begin{aligned} n &= \frac{m}{M} \quad &(\text{moli a partire dalla massa});\\ N &= n\, N_\mathrm{A} \quad &(\text{particelle a partire dalle moli});\\ m &= \frac{N}{N_\mathrm{A}} \, M \quad &(\text{massa a partire dal numero di particelle}). \end{aligned} \]
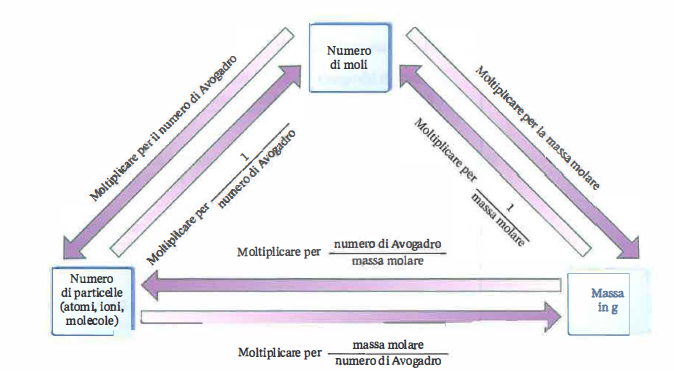
La conversione bidirezionale tra le tre grandezze — massa in grammi, quantità di sostanza in moli, numero di particelle — è riassunta nello schema della (Figura 04.01-02).
Fattori e dati normalmente necessari:
- massa molare \(M\) dell’elemento o composto in g/mol (da tavola periodica o da somma delle masse atomiche per le molecole);
- costante di Avogadro \(N_\mathrm{A} = 6{,}022\,140\,76 \times 10^{23}\ \mathrm{mol^{-1}}\);
- equazione chimica bilanciata, per collegare le moli dei reagenti alle moli dei prodotti.
Esempio 1: da massa a numero di atomi
Quanti atomi sono contenuti in 2,50 g di magnesio?
\[ \begin{aligned} M(\mathrm{Mg}) &\approx 24{,}305\ \mathrm{g\ mol^{-1}};\\ n(\mathrm{Mg}) &= \frac{2{,}50\ \mathrm{g}}{24{,}305\ \mathrm{g\ mol^{-1}}} = 0{,}1029\ \mathrm{mol};\\ N(\mathrm{Mg}) &= 0{,}1029\ \mathrm{mol} \times 6{,}022 \times 10^{23}\ \mathrm{mol^{-1}} \approx 6{,}19 \times 10^{22}\ \text{atomi}. \end{aligned} \]
Esempio 2: da numero di atomi a massa
Qual è la massa di argon che contiene \(3{,}00 \times 10^{22}\) atomi?
\[ \begin{aligned} n(\mathrm{Ar}) &= \frac{3{,}00 \times 10^{22}}{6{,}022 \times 10^{23}}\ \mathrm{mol} = 4{,}984 \times 10^{-2}\ \mathrm{mol};\\ M(\mathrm{Ar}) &\approx 39{,}948\ \mathrm{g\ mol^{-1}};\\ m(\mathrm{Ar}) &= 4{,}984 \times 10^{-2}\ \mathrm{mol} \times 39{,}948\ \mathrm{g\ mol^{-1}} \approx 1{,}99\ \mathrm{g}. \end{aligned} \]
Esempio 3: molecole e conteggio di atomi
In 0,250 mol di \( \mathrm{CO_2} \) quante molecole e quanti atomi di ossigeno sono presenti?
\[ \begin{aligned} N(\mathrm{CO_2}) &= 0{,}250\ \mathrm{mol} \times 6{,}022 \times 10^{23}\ \mathrm{mol^{-1}} = 1{,}5055 \times 10^{23}\ \text{molecole};\\ N(\text{atomi di O}) &= 2 \times N(\mathrm{CO_2}) = 3{,}011 \times 10^{23}\ \text{atomi di O}. \end{aligned} \]
Questi strumenti permettono di progettare in modo quantitativo i processi: dalla massa desiderata di prodotto si risale, tramite i rapporti stechiometrici dell’equazione chimica, alle moli e quindi alle masse dei reagenti necessari, valutando anche costi e rese operative. L’intero procedimento poggia su due pilastri: il bilanciamento corretto dell’equazione e l’uso coerente di mole, massa molare e costante di Avogadro.